- `
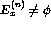 (n fixed).
(n fixed). - `
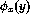 is a perfect square'.
is a perfect square'. - `n is a Fermat's number'. (we say the n is a Fermat's
number if there are numbers x,y,z ;SPMgt; 0 such that
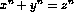 .).
.). - `there is a run of x consecutive 7's in the decimal expansion
of
 '.
'.
- `
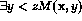 ' is partially decidable.
' is partially decidable. - `
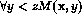 ' is partially decidable.
' is partially decidable. - `
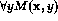 ' is not necessarily partially
decidable.
' is not necessarily partially
decidable.
- `x is even'
- `x divides y'
- Suppose that M(x) is a predicate and k a total
computable function such that
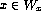 iff M(k(x)) does
not hold. Prove that M(x) is not partially decidable.
iff M(k(x)) does
not hold. Prove that M(x) is not partially decidable. - Prove that `
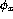 is total' is not partially decidable.
is total' is not partially decidable. - By considering the function
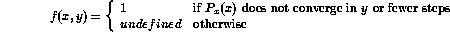
show that `
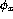 is total' is not partially decidable.
[Hint: use s-m-n theorem and (a)].
is total' is not partially decidable.
[Hint: use s-m-n theorem and (a)].
![]()
is partially decidable. (we take this to mean that ![]() does
not hold if any one of
does
not hold if any one of ![]() is
undefined.)
is
undefined.)