Recursive and recursively enumerable sets

1. Let A, B be subsets of . Define and by

   

   where defined before. Prove that

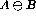   1. is recursive iff both A and B are recursive.
   2. If 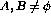, then 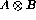is recursive iff both A and B are recursive.
2. Let and let n ;SPMgt; 1. Prove that if B is recursive then the predicate given by given by

   

   is decidable.

3. Let . Prove that A is recursive iff is recursive.
4. For any , let . Show that is r.e for all a. Does the enumeration include all r.e. sets?
5. Show that the set is r.e.
6. Show that there are total computable functions k,l such that for every x, and .
7. Suppose that A is an r.e set. Show that the sets and are both r.e. Show that is not necessarily r.e. as follows. For ant t let . Show that for ant t, is recursive; moreover and .
8. Let f be a unary computable function, and suppose that , and let . Prove that g is computable iff A is r.e.
9. Let f is a unary function. Prove that f is computable iff the set is r.e.
10. Let A be an inifinite r.e. set. Show that A can be enumerated without repetitions by a total computable function.
11. Which of the following sets are recursive? Which are r.e.? Which have r.e. complement?
    1. 
    2. 
    3. 
    4. 
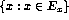
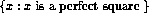
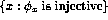
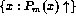    5. (m is fixed)
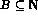12. 1. Let and let n ;SPMgt; 1. Prove that id B is r.e then the predicate 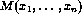given by

       

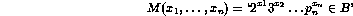
       is partially decidable.

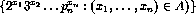    2. Let . Prove that A is r.e. iff is r.e..
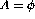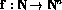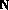    3. Prove that is r.e. iff or there is a total computable function such that A = Ran(f). (By a total computable function from to 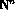we mean an n-tuple 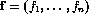where each 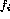is a unary computable function and .)
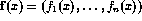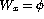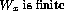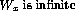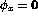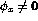13. Suppose that f is a total computable function, A is a recursive set and B is a recursively enumerable set. Show that is recursive and that f(A), f(B) and are r.e. but not necessarily recursive. What extra information can be obtained about these sets if f is a bijection?
14. Use Rice-Shapiro's theorem to show that the following problems are not partially decidable:
    1. ` '
    2. ` '
    3. ` '
    4. ` '
    5. ` '
15. Prove Rice's theorem from the Rice-Shapiro's theorem. [Hint: Suppose that ` ' is decidable. Then both and satisfy the conditions of Rice-Shapiro: consider the cases and .].