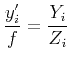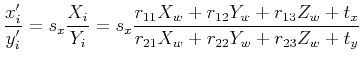- Ignoring radial distortion (for the time being) and setting
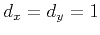 (measuring
(measuring 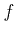 in pixels), we have
in pixels), we have
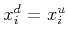 and
and
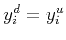 .
.
- Then, combining equations we have
and
- Assuming
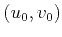 to be known (at the center of the image) and
setting
to be known (at the center of the image) and
setting
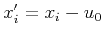 and
and
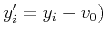 , we have
, we have
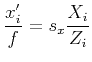
and
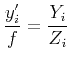
- Eliminating
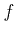 we have
we have
- Rearranging, we have
or
which is a linear homogeneous equation in the eight unknowns
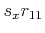 ,
,
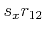 ,
,
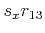 ,
, 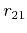 ,
, 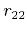 ,
, 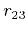 ,
,
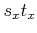 and
and 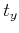 .
.
- The unknown scale factor can be fixed by setting
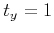 . Image
correspondences of seven points in general position are sufficient to
solve for the remaining unknowns. Let the solution be
. Image
correspondences of seven points in general position are sufficient to
solve for the remaining unknowns. Let the solution be
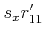 ,
,
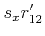 ,
,
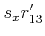 ,
, 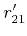 ,
, 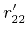 ,
, 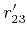 ,
, 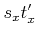 and
and 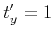
- We can estimate the correct scale factor by noting that the two rows
of the rotation matrix are supposed to be normal, i.e.,
- The scale factor
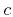 for the solution can then be determined from
for the solution can then be determined from
and
This also allows recovery of 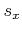 .
.
- In the above procedure we didn't enforce orthogonality of the first
two rows of
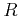 . Given vectors
. Given vectors
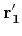 and
and
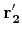 , we can
find two orthogonal vectors
, we can
find two orthogonal vectors 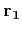 and
and 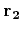 close to the
originals as follows:
close to the
originals as follows:
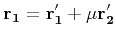
and
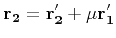
which gives
The solution of this quadratic in 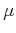 is numerically ill behaved
because
is numerically ill behaved
because
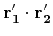 will be quite small. We can
use the approximate solution
will be quite small. We can
use the approximate solution
since
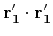 and
and
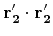 are both near 1.
are both near 1.
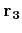 can then be recovered as
can then be recovered as
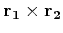 .
.
- Once we have
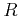 we can estimate
we can estimate 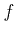 and
and 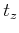 from the basic equations
above. This will require one more correspondence to be given.
from the basic equations
above. This will require one more correspondence to be given.
- The above procedure may be problematic if
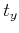 is close to 0. In such
a case the entire experimental data may have to be first translated
by a fixed amount.
is close to 0. In such
a case the entire experimental data may have to be first translated
by a fixed amount.
Subhashis Banerjee
2008-01-20
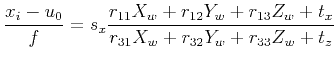
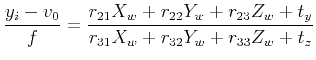
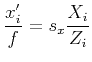 and
and