Next: Camera calibration and absolute Up: Tsai camera model and Previous: Linear estimation of parameters
Finally, using the linear estimates of ![]() ,
, ![]() and
and ![]() as a starting point
one can solve for all the parameters, including the radial lens distortion
parameter
as a starting point
one can solve for all the parameters, including the radial lens distortion
parameter ![]() which was initialized to 0, by minimizing the image
distance
which was initialized to 0, by minimizing the image
distance
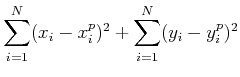
where