 |
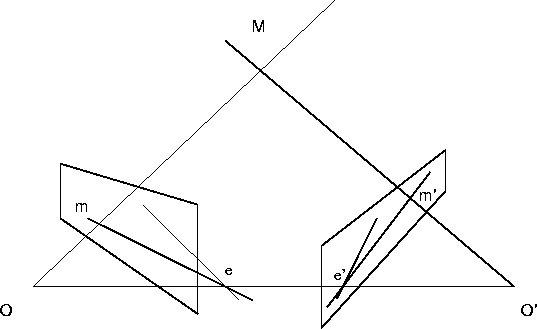
Consider the case of two perspective images of a rigid scene. The
geometry of the configuration is depicted in
fig. 5.1. The 3D point M projects to point m in the
left image and m' in the right one.
Now let M move around in space. The epipolar planes form a pencil of planes through [O,O'], and the epipolar lines form two pencils of lines through e and e' respectively.
Key Property: The epipolar line-line and line-plane correspondences are projective.
Proof: Perspective projection through any third point on [O,O']provides the required projective collineation.
![]()
Projectively, the epipolar geometry is all there is to know about a
stereo rig. It establishes the correspondence
![]() ,
and allows 3D reconstruction of the scene to be carried out up to an
overall 3D projective deformation (which is all that can be done
with any number of completely uncalibrated cameras, without further
constraints). An important practical application of epipolar geometry
is to aid the search for corresponding points, reducing it from the
entire second image to a single epipolar line. The epipolar geometry
is sometimes obtained by calibrating each of the cameras with respect
to the same 3D frame, but as the next section shows, it can easily be
found from a few point correspondences, without previous camera
calibration.
,
and allows 3D reconstruction of the scene to be carried out up to an
overall 3D projective deformation (which is all that can be done
with any number of completely uncalibrated cameras, without further
constraints). An important practical application of epipolar geometry
is to aid the search for corresponding points, reducing it from the
entire second image to a single epipolar line. The epipolar geometry
is sometimes obtained by calibrating each of the cameras with respect
to the same 3D frame, but as the next section shows, it can easily be
found from a few point correspondences, without previous camera
calibration.