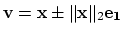

Next: About this document ...
Up: CSL361 Problem set 5:
Previous: Least-squares
Let
be a subspace.
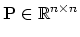 is the
orthogonal projection onto
is the
orthogonal projection onto 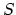 if
if
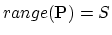 ,
,
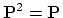 and
and
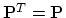 .
.
- Show the following:
- If
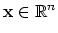 and
and 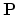 is an orthogonal
projection on to
is an orthogonal
projection on to 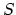 (
(
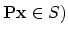 , then
, then
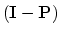 is an orthogonal projection onto
is an orthogonal projection onto
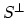 (
(
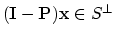 ) where
) where
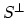 is the orthogonal complement of
is the orthogonal complement of 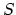 .
.
- The orthogonal projection onto a subspace is unique.
- If
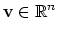 , then
, then
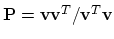 is the
orthogonal projection onto
is the
orthogonal projection onto
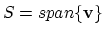 .
.
- If the columns of
![$ {\bf V} = \left[ {\bf v_1},\ldots,{\bf v_k}\right]$](img96.png) are an orthonormal basis for
are an orthonormal basis for 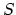 , then
, then
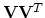 is the unique
orthonormal projection onto
is the unique
orthonormal projection onto 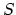 .
.
- Suppose that the SVD of
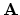 is
is
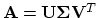 and
and
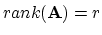 .
If we have the
.
If we have the 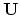 and
and 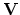 partitionings:
partitionings:
Then, show that
-
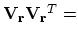 projection onto
projection onto
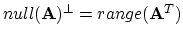
-
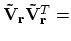 projection onto
projection onto
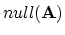
-
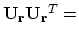 projection onto
projection onto
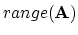
-
projection onto
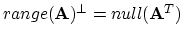
- Let
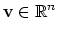 be non-zero. The
be non-zero. The
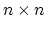 matrix
is the Householder reflection discussed in class.
Show that:
matrix
is the Householder reflection discussed in class.
Show that:
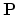 is an orthogonal projection.
is an orthogonal projection.
- When a vector
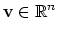 is multiplied by
is multiplied by 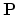 ,
it is reflected in the hyperplane
.
,
it is reflected in the hyperplane
.
- If
Then,

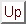

Next: About this document ...
Up: CSL361 Problem set 5:
Previous: Least-squares
Subhashis Banerjee
2005-10-03
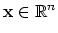 and
and 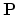 is an orthogonal
projection on to
is an orthogonal
projection on to 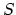 (
(
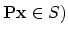 , then
, then
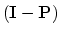 is an orthogonal projection onto
is an orthogonal projection onto
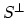 (
(
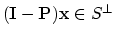 ) where
) where
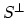 is the orthogonal complement of
is the orthogonal complement of 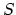 .
.
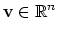 , then
, then
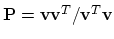 is the
orthogonal projection onto
is the
orthogonal projection onto
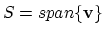 .
.
![$ {\bf V} = \left[ {\bf v_1},\ldots,{\bf v_k}\right]$](img96.png) are an orthonormal basis for
are an orthonormal basis for 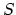 , then
, then
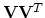 is the unique
orthonormal projection onto
is the unique
orthonormal projection onto 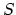 .
.
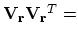 projection onto
projection onto
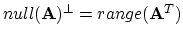
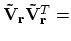 projection onto
projection onto
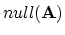
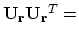 projection onto
projection onto
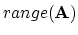
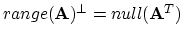
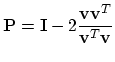
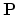 is an orthogonal projection.
is an orthogonal projection.
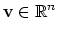 is multiplied by
is multiplied by 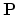 ,
it is reflected in the hyperplane
.
,
it is reflected in the hyperplane
.