Find the least-squares solution to the
Show that the following constitute a solution:
- Find the SVD
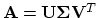
- Set
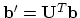
- Find the vector
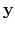 defined by
defined by
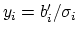 ,
where
,
where 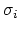 is the
is the 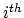 diagonal entry of
diagonal entry of
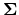
- The solution is
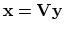
Find the general least-squares solution to the
Show that the following constitute a solution:
- Find the SVD
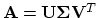
- Set
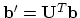
- Find the vector
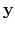 defined by
defined by
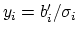 ,
for
,
for
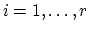 , and
, and 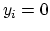 otherwise.
otherwise.
- The solution
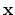 of minimum norm
of minimum norm
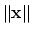 is
is 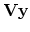
- The general solution is
where are the last columns of
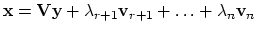
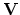 .
.
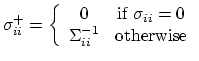
Given
Show that the solution is given by the last column of
Show that a solution is given as:
- If
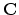 has fewer rows than columns, then add
has fewer rows than columns, then add
 rows to
rows to 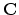 to make it square. Compute the
SVD
to make it square. Compute the
SVD
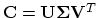 . Let
. Let
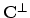 be the matrix obtained from
be the matrix obtained from 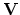 after
deleting the first
after
deleting the first 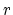 columns where
columns where 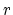 is the number of
non-zero entries in
is the number of
non-zero entries in
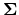 .
.
- Find the solution to minimization of
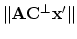 subject to
.
subject to
.
- The solution is obtained as
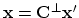 .
.
Show that a solution is given as:
- Compute the
SVD
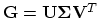 . Let
. Let
- Let
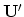 be the matrix of first
be the matrix of first 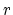 columns of
columns of
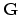 where
.
where
.
- Find the solution to minimization of
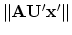 subject to
subject to
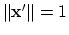 .
.
- The solution is obtained as
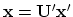 .
.