- lines:
- Let
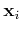 be a set of points on a line
be a set of points on a line 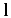 and
consider the action of a
and
consider the action of a
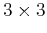 projective transformation
projective transformation  on the the points. Since the points lie on the line we have
on the the points. Since the points lie on the line we have
One can easily verify that
Thus the points
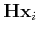 all lie on the line
all lie on the line
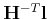 .
Hence, if points are transformed as
.
Hence, if points are transformed as
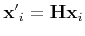 , lines are transformed
as
, lines are transformed
as
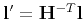 .
.
- conics:
- Note that a conic is represented (homogeneously) as
Under a point transformation
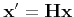 the
conic becomes
the
conic becomes
which is the quadratic form of
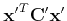 with
with
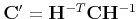 . This gives the transformation rule for a conic.
. This gives the transformation rule for a conic.
Subhashis Banerjee
2008-01-20