Lines and conics in

Lines and conics in ${\cal P}^2$

A line equation in $\mathbb{R}^2$ is

$\displaystyle a_1 x_1 + a_2 x_2 + a_3 = 0$
Substituting by homogeneous coordinates we get a homogeneous linear equation

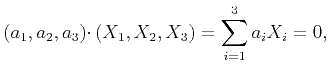
$\displaystyle (a_1,a_2,a_3) \cdotp (X_1,X_2,X_3) = \sum_{i=1}^{3} a_i X_i = 0,$ $\displaystyle {\bf X} \in {\cal P}^2$
A line in ${\cal P}^2$ is represented by a homogeneous 3-vector .
A point on a line:

$\displaystyle {\bf a} \cdotp {\bf X} = 0$ or $\displaystyle {\bf a}^T {\bf X} = 0$ or $\displaystyle {\bf X}^T {\bf a} = 0$
Two points define a line:

$\displaystyle {\bf l} = {\bf p} \times {\bf q}$
Two lines define a point:

$\displaystyle {\bf x} = {\bf l} \times {\bf m}$
Matrix notation for cross products:
The cross product ${\bf v} \times {\bf x}$ can be represented as a matrix multiplication

$\displaystyle {\bf v} \times {\bf x} = \left[ {\bf v} \right]_{\times} {\bf x}$

where $\left[ {\bf v} \right]_{\times}$ is a $3 \times 3$ antisymmetric matrix of rank 2:

$\displaystyle \left[ {\bf v} \right]_{\times} = \left[ \begin{array}{ccc} 0 & -v_z & v_y \\ v_z & 0 &-v_x \\ -v_y & v_x & 0 \end{array}\right]$
The line at infinity ( ${\bf l}_\infty$ ): is the line of equation . Thus, the homogeneous representation of ${\bf l}_\infty$ is .
The line intersects ${\bf l}_\infty$ at the point .
Points on ${\bf l}_\infty$ are directions of affine lines in the embedded affine space (can be extended to higher dimensions).
Consider the standard hyperbola in the affine space given by equation . To transform to homogeneous coordinates, we substitute and to obtain . This is homogeneous in degree 2. Note that both $(0,\lambda,0)$ and $(\lambda,0,0)$ are solutions. The homogeneous hyperbola crosses the coordinate axes smoothly and emerges from the other side. See the figure.

$\includegraphics{hyperbole.ps}$
A conic in affine space (inhomogeneous coordinates) is

$\displaystyle ax^2 + bxy + cy^2 + dx + ey + f = 0$

Homogenizing this by replacements and , we obtain

$\displaystyle aX_1^2 + bX_1X_2 + cX_2^2 + d X_1X_3 + e X_2X_3 + f X_3^2 = 0$

which can be written in matrix notation as

$\displaystyle {\bf X}^T{\bf C}{\bf X} = 0$

where is symmetric and is the homogeneous representation of a conic.

$\displaystyle C = \left[ \begin{array}{ccc} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{array}\right]$
Five points define a conic.
The line ${\bf l}$ tangent to a conic ${\bf C}$ at any point ${\bf x}$ is given by ${\bf l} = {\bf C}{\bf x}$ .
$\displaystyle {\bf x}^t{\bf Cx} = 0 \implies ({\bf C}^{-1}{\bf l})^t{\bf C}(({\bf C}^{-1}{\bf l}) = {\bf l}^t{\bf C}^{-1}{\bf l} = 0$

(because ${\bf C}^{-t} = {\bf C}^{-1}$ ). This is the equation of the dual conic.

$\includegraphics[width=0.4\textwidth]{fig1.2a.ps}$ $\includegraphics[width=0.4\textwidth]{fig1.2b.ps}$
The degenerate conic of rank 2 is defined by two line ${\bf l}$ and ${\bf m}$ as

$\displaystyle {\bf C} = {\bf lm}^t + {\bf ml}^t$

Points on line ${\bf l}$ satisfy ${\bf l}^t{\bf x} = 0$ and are hence on the conic because $({\bf x}^t{\bf l})({\bf m}^t{\bf x}) + ({\bf x}^t{\bf m})({\bf l}^t{\bf x}) = 0$ . (Similarly for ${\bf m}$ ).
The dual conic ${\bf x}{\bf y}^t + {\bf y}{\bf x}^t$ represents lines passing through ${\bf x}$ and ${\bf y}$ .

Subhashis Banerjee 2008-01-20