Minor II Solutions

1. 1. Construct

      

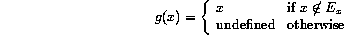
      g is computable if 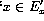is decidable. Clearly, Range of g is different from that of every computable function. Let 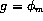. Then

      

      Thus we have a contradiction.

   2. Suppose 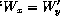is decidable. Then so is 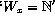. But .
2. Suppose that f is computable. Then there is a program P that computes it. We have that

   

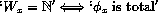   The predicate on the RHS is partially decidable by Theorem done in the class.

   Conversely, suppose that the predicate is partially decidable. Let be a decidable predicate such that

   

   Then we have the following algorithm for computing f. Search for a pair of numbers y,t such that holds; if and when such a pair is found then . Hence f is computable. [Note that in the usual way a search over y,t can be conducted by coding the pair as a single number .]

3. Given that f is a total computable function, A is a recursive set and B is a recursively enumerable set.

   Now, ; since f is total computable, f(x) is defined and is decidable because A is recursive. We have that . Hence is recursive.

   f(A) and f(B) are ranges of a total unary computable function. Hence these sets are recursively enumerable. However, f is not necessarily a total increasing computable function; consequently, f(A) and f(B) are not necessarily recursive.

   Now, B is recursively enumerable. Hence it is the range of a total unary computable function, say g. Now, . Now since both f and g are total computable, the predicate `f(x) = g(y)' is decidable. Thus is partially decidable, which in turn implies that is recursively enumerable. This set is recursive only if g is increasing.

   If f is a bijection then is also total computable but not necessarily monotonic. Thus '. Since A is recursive so is f(A). But since neither f nor are monotonic f(B) and are not necessarily recursive.

4. 1. Define .
      

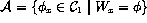      Let this set be r.e. If this set is r.e. then according to Rice-Shapiro's theorem: `if there exists a finite 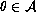, 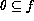for some computable f, then '.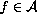

      Let f be a total computable function. Clearly 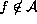. Let 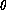be the function which is nowhere defined. Clearly 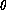is of finite domain and trivially 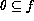. Also 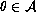. Thus we have a contradiction.

   2. Define .
      

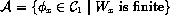      Let this set be r.e. If this set is r.e. then according to Rice-Shapiro's theorem: `if there exists a finite 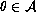, 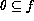for some computable f, then '.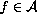

      Let f be a total computable function. Let 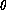be any finite restriction of f. Clearly 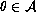and 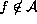. Thus we have a contradiction.

   3. Define .

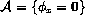      Let this set be r.e. If this set is r.e. then according to Rice-Shapiro's theorem: `if 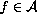then there must exist a finite 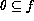such that '.

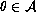      But no finite function can be the function . Thus we have a contradiction.

• About this document ...