


Next: About this document ...
CS130N Problem set 4: BST and height balancing
- 1.
- Write out algorithms for following operations on a binary search
tree: search, finding maximum and minimum, insertion and deletion.
Assuming that the height of the BST is O(h), estimate the
time requied for each of these operations.
- 2.
- Repeat that analysis done in the class to show that if the
input tokens arrive at random according to uniform distribution,
then, on the average, the height of a binary search tree
is
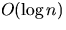 .
. - 3.
- Derive the average case recurrence for Quicksort and show the
similarities with the recurrence derived in the previous problem.
Why are the recurrences similar?
- 4.
- Draw the complete binary tree of height 3 on the keys
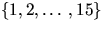 . Add the NIL leaves and colour the nodes in three different ways
such that the black heights of the resulting Red-Black trees are
2, 3 and 4.
. Add the NIL leaves and colour the nodes in three different ways
such that the black heights of the resulting Red-Black trees are
2, 3 and 4.
- 5.
- Suppose that root of a Red-Black tree is red. If we make it black,
does the tree remain a Red-Black tree?
- 6.
- Show that the longest simple path from a node x in a Red-Black tree
to a descendant leaf has length at most twice that of the shortest
simple path from node x to a descendant leaf.
- 7.
- What is the largest possible number of internal nodes in a
red-black tree with black height k? What is the smallest possible
number?
- 8.
- Describe a Red-Black tree on n keys that realizes the largest possible
ratio of red internal nodes to black internal nodes. What is this ratio?
What tree has the smallest possible ratio? What is the ratio?
- 9.
- Construct an algorithm for deleting a node in a RB tree and show that
this can be accomplishes in
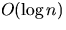 steps.
steps.
- 10.
- Study the algorithms for insertion and deletion in an AVL tree.
- 11.
- What is the worst case example of a height balanced tree?



Next: About this document ...
Subhashis Banerjee
2/19/2001