![]()
- (a)
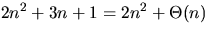
- (b)
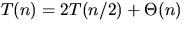 (why is it acceptable
not to write the base case for this recurrence?)
(why is it acceptable
not to write the base case for this recurrence?)
- (c)
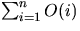
- (d)
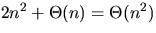
We prove ![]() . We obviously have the base case. Now,
. We obviously have the base case. Now,
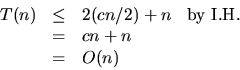
- (a)
- f(n) = n
- (b)
- f(n) = n4
- (c)
- f(n) = 2n
- (d)
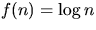
- (e)
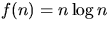
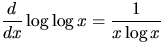 to show that
to show that
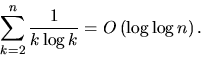
- (a)
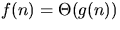 and
and 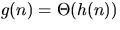 implies
implies 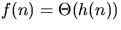 .
.- (b)
- f(n) = O(g(n)) and g(n)=O(h(n)) implies f(n)=O(h(n)).
- (c)
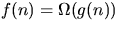 and
and 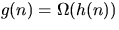 implies
implies 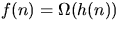 .
.- (d)
- f(n) = O(g(n)) implies g(n) = O(f(n)).
- (e)
- f(n) = O(g(n)) iff
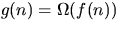 .
. - (f)
- f(n) = O(g(n)) implies
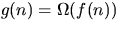 .
. - (g)
- f(n) = O(g(n)) implies 2f(n)=O(2g(n)).
- (h)
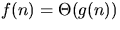 iff
iff 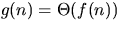
T(n) = aT(n/b) + f(n)
where we interpret n/b to mean either- (a)
- If
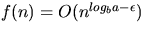 for some
for some 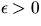 ,then
,then 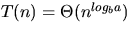 .
. - (b)
- If
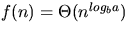 , then
, then

- (c)
- If
 for some
for some 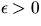 , and if
, and if  for some c < 1 and all sufficiently
large n, the
for some c < 1 and all sufficiently
large n, the  .
.