


Next: About this document ...
Data Structures (CS130N) Minor II March 20, 2001
Name: Entry: Grp:
Note:
Maximum marks : 60 (a mark a minute). All questions carry equal marks. Answer only in the space provided.
2 pages in all.
- 1.
- Describe an algorithm to find the inorder successor of a given node x
in an AVL tree.
- 2.
- Let D be an ordered dictionary with n items implemented by means
of an AVL tree. Show how to implement the operation
findAllInRange(k1,k2) (which returns an enumeration of all the
elements in the D with key k such that
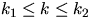 ) on D in time
) on D in time 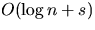 , where s is the size of the enumeration
returned.
, where s is the size of the enumeration
returned.
- 3.
- Suppose that the number of elements n to be inserted in a hash
table (assume chaining and universal hashing) is not known in advance.
We can then construct a sequence
of hash tables
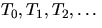 as follows. We choose some
initial value N for the initial hash table T0. Then, when
the number of elements inserted in T0 exceeds N, we create
a new hash table T1 of size 2N and by rehashing (choose a new
universal hash function) move all
elements of T0 in to T1. T0 can now be discarded. We can then
insert new elements in to T1
till the number of elements exceed 2N. In general, we create
a table Tk of size 2k N as soon as table Tk-1 contains
2k-1N elements. Derive the expected time for insertion of
n elements using the above procedure.
as follows. We choose some
initial value N for the initial hash table T0. Then, when
the number of elements inserted in T0 exceeds N, we create
a new hash table T1 of size 2N and by rehashing (choose a new
universal hash function) move all
elements of T0 in to T1. T0 can now be discarded. We can then
insert new elements in to T1
till the number of elements exceed 2N. In general, we create
a table Tk of size 2k N as soon as table Tk-1 contains
2k-1N elements. Derive the expected time for insertion of
n elements using the above procedure.
- 4.
- Dean Prasad wants to keep the motivation levels of students
of CS130N high by giving incentives. He has suggested that after
the second minor the top
 students be distributed samosas
and the next
students be distributed samosas
and the next 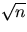 students be given gulab jamuns. However, he
has stipulated that we cannot sort the student roll list according
to marks (which would take
students be given gulab jamuns. However, he
has stipulated that we cannot sort the student roll list according
to marks (which would take 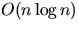 time) but should use our
data structures skills to determine who gets what in O(n) time.
time) but should use our
data structures skills to determine who gets what in O(n) time.



Next: About this document ...
Subhashis Banerjee
4/24/2001