Lecture 18
Core in Cooperative Games

Scribed By: Deepak Sethi

October 16, 2002


Contents

Review of the Previous Lecture

In the games we have discussed so far we assumed that the utilities specified for the players can't be transfered among the themselves, i.e to say that all the players play for themselves and they do not share their gain with others.

Now we are interested in analysing games in which players can form group among themselves and can transfer the utilities among the group.Speaking more formally we are interested in analysing "cooperative games with transferable utilies".

A cooperative game is the one, where different players may form alliance with each other in a way to influence the outcome of the game in their favour. A game with transeferable utilities is one where players can share(transfer) their gains(utilities) with other players.

We saw that in non-cooperative games Nash and Stackelberg equilibrium were reasonable solution concepts for the games.Now with cooperative games we will need to device some other solution concept.

Stablitiy in Assignment Game

In the lecture on stable marriages we saw that if a matching is not stable how it can be destablaised by a pair.

We can see a similar analogy in the the assignement game where a set of custiomers {A, B ...} have to be assigned one item each from the set {$\alpha, \beta $...}.

The utility of an item for customer is given by the weight of the edge connecting the customer to the seller of that particular item. The seller of the item is assumed to have a cost of zero for each item i.e. he is willing to sell them at any price.

The payoff for the seller is given by the difference between the price the item fetches , and it's cost.Similarily for the customer the payoff is the difference between the utility and it's cost.

Now consider the following scenario:

Customer A values item $\alpha$ at 10 and $\beta$ at 15.

Customer B values item $\beta$ at 10 and $\alpha$ at 0.

A is assigned $\alpha$ at a price 4 and B is assigned $\beta$ at price 7.

\includegraphics[width=0.75\textwidth,height=0.5\textwidth]{ass1}
In this assignment the payoff for A is 6 whereas the payoff for $\beta$ is 7.

The above assignment is not stable as the assignmenet of $\beta$ to A at a price 8 of would have been more profitable for A and the seller of $\beta$ as this assignment would increase the payoff of both of them as compared to the previous assignment.

This means that if A and $\beta$ cooperate and play this game then both of them can increase their payoffs therefore the assignment that was shown earlier was not stable.

In fact, for the assignment game no price distribution will be stable if it makes the sum of payoffs of the nodes on the edge less than the weight of the edge (assuming that the cost of the item is zero for the seller)..!

Now we would like to analyse the possible set of stable outcomes of such a game. Core and Stable sets are two such mechanisms for analysing the outcomes of cooperative games with transferable utilities.

Let us now start with some definitions for formalizing the concept of the core and stable sets:

Characterisitc Function

Suppose that the players play a cooperative game to finally arrive at an outcome $\omega$. Now the value of this outcome is defined by:


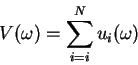
\begin{displaymath} V(\omega)=\sum_{i=i}^{N}u_{i}(\omega) \end{displaymath}

where N is the number of players in the game and let the utility for the player i at an outcome $\omega$ is given by $u_{i}$.

Let $\omega^{*}$ be the outcome that has the maximum value.i.e.

\begin{displaymath} \omega^{*} = arg \max_{\omega}V(\omega) \end{displaymath}

We denote the set of players by $\mathcal{N}$.

Define the value of the game with players in $\mathcal{N}$ cooperating be

\begin{displaymath} \mathcal{V}(\mathcal{N}) = V(\omega^{*}) \end{displaymath}

Similarily for a subset $\mathcal{S}\subseteq\mathcal{N}$ we can define the value as,

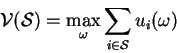
\begin{displaymath} \mathcal{V}(\mathcal{S}) = \max_{\omega} \sum_{i\in\mathcal{S}} u_{i}(\omega) \end{displaymath}

assuming that it only players in set $\mathcal{S}$ are playing the game among themselves and are not interacting with other players in the set $\mathcal{N}-\mathcal{S}$. Function $\mathcal{V}$ is called the charateristic function for the game since it contains all the information required about the game in itself.

Another way to understand the characteristic function is by the following definition:

$\mathcal{V}(\mathcal{S}) =$ Best payoff if the players in set $\mathcal{S}$ cooperate.

We assume the following properties for the characteristic function:

Now we are interested in definig the stability of an outcome for an N player cooperative game.

Stability and core in cooperative games

Define $\pi$ as a payoff division for an outcome $\omega$ if

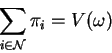
\begin{displaymath} \sum_{i\in\mathcal{N}}\pi_{i} =V(\omega) \end{displaymath}

Thus

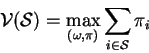
\begin{displaymath} \mathcal{V}(\mathcal{S})=\max_{(\omega,\pi)}\sum_{i\in\mathcal{S}}\pi_{i} \end{displaymath}

We say that subset $\mathcal{S}$ of the players can destabalize the outcome $(\omega,\pi)$ if


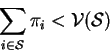
\begin{displaymath} \sum_{i\in\mathcal{S}}\pi_{i} < \mathcal{V}(\mathcal{S}) \end{displaymath}

The above condition means that if the players in the set $\mathcal{S}$ cooperate among themselves then they can get a better payoff than what the outcome $(\omega,\pi)$ is giving to them .So they can be better off if they cooperate among themselves and play the game and then share their payoffs.

Define an imputation $\pi$ as a payoff divison for which:

\begin{displaymath} \pi_{i} > \mathcal{V}(\{i\}) \end{displaymath}


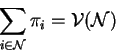
\begin{displaymath} \sum_{i\in\mathcal{N}} \pi_{i} = \mathcal{V}(\mathcal{N}) \end{displaymath}

An Imputation $\pi$ is said to be in the core of a game iff no $\mathcal{S}\subset\mathcal{N}$ can destablize the outcome with imputation $\pi$.

Formally $\pi$ is in core iff:

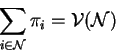
\begin{displaymath} \sum_{i\in\mathcal{N}} \pi_{i} = \mathcal{V}(\mathcal{N}) \end{displaymath}


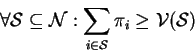
\begin{displaymath} \forall \mathcal{S}\subseteq\mathcal{N} : \sum_{i\in\mathcal{S}} \pi_{i} \geq \mathcal{V}(\mathcal{S}) \end{displaymath}

Thus, we see that the imputation $\pi$ is in the core of the game if it prevents the players from forming small coalitions by paying off all the subsets an amount which is at least as much they would get if they form a coalition.

Thus the core of a game is a set of imputations which are stable.

But now the big question is whether the core always exists? We answer the above question by means of examples.

Illustrative Examples

Shortest Path Routing

Consider the game in which a sender has to transport the traffic from node s to node t in the following network.Assume that each link is owned by an individual and player. The owner of each link incurs some cost while transporting traffic along its link which is denoted by the number written over the edge.

We will consider two distinct examples of this game one in which the game has a core consisting of a single imputation and the other with the core consisting of multiple imputations.

Single Imputation Core

\includegraphics[width=0.75\textwidth,height=0.5\textwidth]{graph1}

We see that in this game the buyer and the owners of the links are the players.

Assume that the sender(buyer) makes a payment $P_{i}$ to the owner of link i. So the total payment P made by the sender is given by:

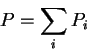
\begin{displaymath} P=\sum_{i}P_{i} \end{displaymath}

Let us also assume that the payoff for the players is as follows:

We claim that the above game has the core consisting of a single imputation which gives a payoff of 10 to the sender and zero to all the link owners.

We prove the above claim by the following argument.

First of all we note that $\mathcal{V}(\mathcal{N})=10$ for this game. The cost of all the possible paths is 10. The sender can pay an amount less than 20 or else he would better choose not to send traffic...!

Now note that the in this game $\mathcal{V}(\mathcal{S})=0$ if $sender\notin\mathcal{S}$, as without the sender there would be no traffic to be sent and hence no payoff will be generated.

Also note that if the payoff of any link owner is positive then the sender can cooperate with any two of the four other link owners whose links are presently unused in such a way that the payoff of the sender as well as the link owner get increased.

Illustratively suppose that owner of link A has a payoff of $\epsilon$. This implies that the traffic is being routed through A-B and thereof presently the payoff of C and D is each zero and the payoff for the sender is 10-$\epsilon$. Now if the sender cooperates with the link owners of C and D in such a way that the pair each gets a payoff of $\epsilon/4$ then the payoff of C and D each has increased from zero to $\epsilon/4$ and that of the sender has increased from 10-$\epsilon$ to 10-$\epsilon/2$. Thus the coalition of sender with C and D can destablize the outcome which gives a payoff of $\epsilon$ to A. Similar arguments can be given for the positve outcomes of other link owners as well.

Thus we see that for a outcome to be stable the outcome should give a zero payoff to each of the link owners and hence should give a payoff of 10 to the sender...!

It is also worth noting that the outcome generated by the VCG procedure would give a payoff vector which is the same as the core of this game.

Core with multiple imputations

Now consider the following configuration of the network:
\includegraphics[width=0.75\textwidth,height=0.5\textwidth]{graph2}
As in the previous game the buyer and the owners of the links are the players. Also the payoff for the players is same as before.

The only difference now is that the various possible paths are now of different costs.

Let us first analyse the characteristic function for this game:

Now we will show that for a payoff $\pi$ to be in core it must satisfy the follwing properties: So now we can say that the core of the game consists of the set of payoff $\pi$ which satisfy the following properties.

Note that the payment made by the VCG procedure do not lie in the core. These payments will be 7 to link E and 4 to link F so that the payoff of E is 2 and also the payoff of F is 2 whereas the payoff of the sender is just 9 in this case...!

Now consider a slight variant of the above graph

\includegraphics[width=0.75\textwidth,height=0.5\textwidth]{graph3}
In this graph we can obtain by a similar analysis the core to be the set of payoff vectors $\pi$ which satisfy the following properties:

In this case we see that the outcome obtained by VCG procedure lies on the boudary of the core...!

The Stable Roommate Game

In this game three students {A, B, C} have to live in a hostel which has two types of rooms ,single-bed rooms and double-bed rooms. The single-bed rooms have a rent of Rs 1500/- per room. The double-bed rooms have a rent of Rs 2000/- per room.

We claim that this game has no core.
We prove it in the following manner. There are three posibilities:

Thus we see that this game has no core.

Deepak Sethi 2002-11-22