The poset is : (A) not a lattice (B) a lattice but not a distributive lattice
(C) a distributive lattice but not a Boolean algebra (D) a Boolean algebra
Q.8. Let A, B and C be non-empty sets and let
X = ( A - B ) - C and Y = ( A - C ) - ( B - C )
Which one of the following is TRUE?
(A) X = Y
(B) X ⊂ Y
(C) Y ⊂ X
(D) None of these
Sol : We know that (A - B) = A ∩ B', where B' is complement of set B.
So X = (A - B) - C = (A ∩ B') ∩ C' = A ∩ B' ∩ C'
Also Y = ( A - C ) - ( B - C ) = (A ∩ C') ∩ (B ∩ C')' = (A ∩ C') ∩ (B' ∪ C) = (A ∩ C' ∩ B') ∪ (A ∩ C' ∩ C) = (A ∩ C' ∩ B') ∪ (A ∩ φ) = (A ∩ C' ∩ B') ∪ φ = (A ∩ C' ∩ B') = X
So answer is option (A).
Q.9. The following is the Hasse diagram of the poset [{a,b,c,d,e},≺]
The poset is :
(A) not a lattice
(B) a lattice but not a distributive lattice
(C) a distributive lattice but not a Boolean algebra
(D) a Boolean algebra
Sol : This poset (called M3) is one of the two very popular example of poset which is a lattice, but not distributive lattice. So answer is option (B), but anyway, let us see why.
So a poset is a lattice if, for every two elements a and b, there is a supremum (least upper bound) and an infimum (greatest lower bound).
This poset is a lattice, because every pair has supremum and infimum. For example, (e,b) has supremum as a, and infimum as e.
Now a lattice is distributive if it follows distributive law x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z), and x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z). Here ∧ is infimum operation, and ∨ is supremum operation.
Now this lattice doesn't satisfy this distributive property, because let x = b, y = c, z = d. Then
L.H.S. = x ∧ (y ∨ z) = b ∧ (c ∨ d) = b ∧ a = b
Q.10. Let G be a simple connected planar graph with 13 vetices and 19 edges. Then,
the number of faces in the planar embedding of the graph is:
(A) 6
(B) 8
(C) 9
(D) 13
Sol : This is direct application of euler's formula v + f - e = 2. Here v = 13, e = 19, so f = 8. So option (B) is correct.
Q.11. Let G be a simple graph with 20 vertices and 100 edges. The size of the
minimum vertex cover of G is 8. then, the size of the maximum independent set
of G is:
(A) 12
(B) 8
(C) less than 8
(D) more than 12
Sol : Minimum vertex cover of a graph means minimum set of vertices such that every edge of G has atleast one vertex
in this set. For example in traingle graph shown below, minimum vertex cover is {a,b}, because all three edges ab, bc, and ca
have atleast one vertex in this set. Similarly {b,c} and {a,c} are also minimum vertex set. Moreover, {a} is not vertex set
because it doesn't cover edge bc i.e. none of the vertices of edge bc are in this set. Also, {a,b,c} is a vertex cover, but
not minimum, because we already have vertex cover ({a,b}) of less size.
Independent set of graph is sort of complement of vertex cover. Independent set of a graph is a set of vertices
such that none of the vertices in this set have an edge i.e. they are independent of each other. So by default, set
of single vertex is an independent set, but we are interested in maximum independent set, that is largest set
which is independent set. For example, for above graph, maximum independent set is {a} or {b} or {c}.
Now we come to question. So in question, we are given minimum vertex cover size, and we have to find maximum independent
set size.
Now max independent set size = total no. of vertices - minimum vertex cover size
i.e. vertices which are not in minimum vertex cover form maximum independent set, because suppose if any two vertices in this
independent set had an edge, then one of the them must have been present in vertex cover, which is not the case here.
Moreover, this is maximum because suppose one more vertex was present in this set, then that vertex must come from
vertex cover set (as we don't have extra vertices apart from independent set and vertex cover set), but then that vertex must
had an edge to one of the vertices already present in indpendent set (by definition of vertex cover), which means this set
wouldn't be independent set.
So max independent set size = 20 - 8 = 12, so option (A) is correct.
Q.12. Let f(x) be the continuous probability density function of a random variable X, the probability that a < X ≤ b,
is :
(A) f(b-a)
(B) f(b) - f(a)
(C) \(\int^b_a f(x)\,dx\)
(D) \(\int^b_a xf(x)\,dx\)
Sol : Since X is a continous random variable, P(a < X ≤ b) is area under the curve between a and b i.e. definite integral of function between a and b i.e. $\int^b_a f(x)\,dx$. So option (C) is correct.
Q.13. The set \(\{1, 2, 4, 7, 8, 11, 13, 14\}\) is a group under multiplication modulo 15. the
inverses of 4 and 7 are respectively:
(A) 3 and 13
(B) 2 and 11
(C) 4 and 13
(D) 8 and 14
Sol : Identity element of this group is 1, since every element, when multiplied by 1, gives same element back. Now inverse
of an element is that element, which when multiplied to, gives identity element.
So inverse of 4 is an element x such that \((4*x)mod15 = 1\). Here that x is 4, because \((4*4)mod15 = 1\).
Since only option C has 4, that is the correct answer. Also, we can see that inverse of 7 is 13, because \((7*13)mod15 = 1\).
Q.40. Let P, Q and R be tree atomic prepositional assertions. Let X denote ( P ∨ Q ) → R
and Y denote (P → R) ∨ (Q → R). Which one of the following is a tautology?
(A) X ≡ Y
(B) X → Y
(C) Y → X
(D) ¬Y → X
Sol : First we create the truth table as :
| P | Q | R | X | Y |
|---|---|---|---|---|
| 0 | 0 | 0 | T | T |
| 0 | 0 | 1 | T | T |
| 0 | 1 | 0 | F | T |
| 0 | 1 | 1 | T | T |
| 1 | 0 | 0 | F | T |
| 1 | 0 | 1 | T | T |
| 1 | 1 | 0 | F | F |
| 1 | 1 | 1 | T | T |
Now clearly, we can see that X \(\not\equiv\) Y, but X → Y is true, moreover Y → X is not tautology due to 3rd enrty in table, ¬Y → X is not tautology due to 7th entry in table.
So option (B) is correct.
Q.41. What is the first order predicate calculus statement equivalent to the following?
"Every teacher is liked by some student"
(A) ∀(x)[teacher(x) → ∃(y) [student(y) → likes (y,x)]]
(B) ∀(x)[teacher(x) → ∃(y) [student(y) ∧ likes (y,x)]]
(C) ∃(y) ∀(x)[teacher(x) → [student(y) ∧ likes (y,x)]]
(D) ∀(x)[teacher(x) ∧ ∃(y) [student(y) →; likes (y,x)]]
Sol : So according to statement, we would like to start with ∀(x)[teacher(x) → and not
∀(x)[teacher(x) ∧, because latter would have meant that, every person in this world is teacher, whereas we wanted to say
whoever in this world is teacher, then blah blah. So option (A) is eliminated.
option (C) is also eliminated, because we want to fix some teacher, then want to say about her, not other way around.
Now between option (B) and (D), option (B) is correct, because we want to assert that there is at least a student who
likes teacher. option (D) means if a guy is student, then teacher is liked by that student, so according to D, we may have a
student-less world, and still satisfy the statement, which we don't want here.
So rule of thumb is "use → with ∀ and ∧ with ∃".
Q.42. Let R and S be any two equivalence relations on a non-empty set A. Which one of
the following statements is TRUE?
(A) R ∪ S, R ∩ S are both equivalence relations.
(B) R ∪ S is an equivalence relation.
(C) R ∩ S is an equivalence relation.
(D) Neither R ∪ S nor R ∩ S are equivalence relations.
Sol : R ∩ S is an equivalence relation, because in R ∩ S, we have all pairs of type (a,a) definitely, so R ∩ S is reflexive.
Moreover, if there is any pair (a,b) in R ∩ S, then that must have been present in both R and S, and thus (b,a) must have also been present in both R and S, and so in R ∩ S, so R ∩ S is also symmetric.
We can argue similarly for transitivity. If there are pairs (a,b) and (b,c) in R ∩ S, then they both must have been present in R as well as S, and so (a,c) would have also been present in both R and S, and so (a,c) must also be present in R ∩ S, hence R ∩ S is transitive also.
Now let us see R ∪ S. It is actually not equivalence. The intuition is we may violate the transitivity property because if some (a,b) comes from R, and some (b,c) comes from S, then we will not have (a,c) in R ∪ S (assuming we don't have (a,c) in R or S.
So let us construct a counter example for R∪S to be equivalence statement. Let A = {1,2,3}
Now let R = {(1,1),(2,2),(3,3),(1,2),(2,1)}, and let S = {(1,1),(2,2),(3,3),(2,3),(3,2)}. Now R ∪ S = {(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2)}. This violates transitivity as we have (1,2) and (2,3), but not (1,3).
Q.43. Let f: B → C and g: A → B be two functions let h = \(f\) o \(g\). Given that h is an onto
function which one of the following is TRUE?
(A) f and g should both be onto functions.
(B) f should be onto but g need to be onto
(C) g should be onto but f need not be onto.
(D) both f and g need to be onto.
Sol : Here function h is \(f\) o \(g\), so it takes element of A as input and gives element of C as output. Since
h is given onto, then every element of C must have some pre-image to element of A.
Now function f must be onto, because if it were not onto, it could left out some elements of C, and if it was the case,
then h would have been not onto.
On the other hand, g may not be onto, because it can leave out some elements of B, and still we can map eall elements of A
to some elements of B, and those then can map to all elements of C.
So option (B) is correct.
Q.44. What is the minimum number of ordered pairs of non-negative numbers that
should be chosen to ensure that there are two pairs (a,b) and (c,d) in the chosen
set such that
$$a \equiv c \;mod \;3 \;and \;b \equiv d \;mod \;5$$
(A) 4
(B) 6
(C) 16
(D) 24
Sol : First let us see about \(mod\; 3\). If we answer 2 for this, then I can pick two
pairs, lets say I pick (4,5), and (5,6), but here \(4 \not\equiv 5 \;mod \;3\). So I have to think how many pairs would
ensure that there are some two pairs in them such that their first elements are equivalent mod 3. Mod 3 basically gives remainder
when divided by 3, and we also know that we can get remainder 0, 1, or 2 only for any number.
So we can immediately see that we require 4 pairs, because now no matter which 4 pairs advisory chooses for me, there are two
pairs for which first elements' remainders with 3 are same.
Similarly, for mod 5, we require 6 pairs. So infact, if we answer this question as 16 i.e. (LCM of 3 and 5)+1, both mod 3 and mod 5 requirements would
be fulfilled, so answer is 16 i.e. option (C).
Q.46. Consider the set H of all 3 * 3 matrices of the type
$$\left( \begin{array}{ccc}
a & f & e \\
0 & b & d \\
0 & 0 & c \end{array} \right)$$
where a,b,c,d,e and f are real numbers and abc≠0. under the matrix
multiplication operation, the set H is:
(A) a group
(B) a monoid but not a group
(C) a semi group but not a monoid
(D) neither a group nor a semi group
Sol : So an algebraic structure G, with operation * is a group if satisfies 4 properties :
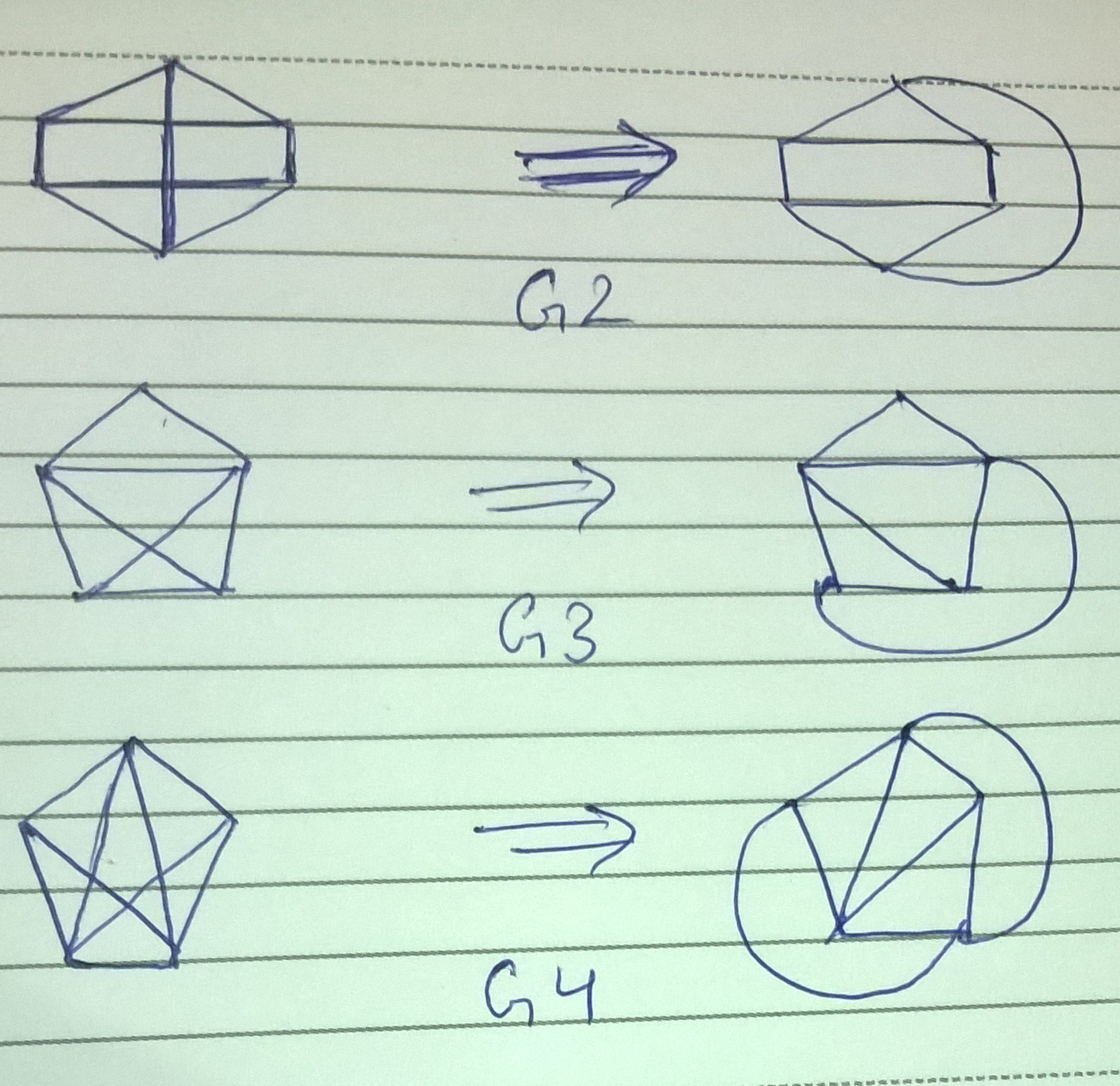
Q.47. Which one of the following graphs is NOT planar?
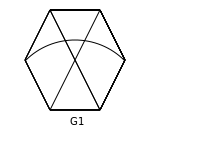
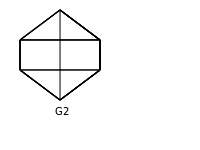
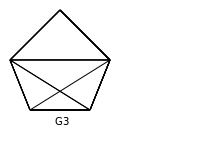
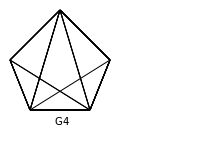
(A) G1
(B) G2
(C) G3
(D) G4
Sol : A graph is planar if it can be drawn on a 2D plane such that no two edges cross each other. So let us try to draw planar graphs corresponding to each graph show in question :
Q.48. Consider the following system of linear equations :
$$2x_1 - x_2 + 3x_3 = 1$$
$$3x_1 + 2x_2 + 5x_3 = 2$$
$$-x_1+4x_2+x_3 = 3$$
The system of equations has
(A) no solution
(B) a unique solution
(C) more than one but a finite number of solutions
(D) an infinite number of solutions
Sol : We write the augmented matrix as :$$\left( \begin{array}{ccc}
2 & -1 & 3 \\
3 & 2 & 5 \\
-1 & 4 & 1 \end{array} \middle\vert \begin{array}{c} 1\\2\\3\end{array}\right)$$
Now we do row operations to bring left matrix to row echelon form.
\(\left( \begin{array}{ccc}
2 & -1 & 3 \\
3 & 2 & 5 \\
-1 & 4 & 1 \end{array} \middle\vert \begin{array}{c} 1\\2\\3\end{array}\right) \xrightarrow{R2\leftarrow R2 - 3/2R1, R3\leftarrow R3 + 0.5R1}
\left( \begin{array}{ccc}
2 & -1 & 3 \\
0 & 7/2 & 0.5 \\
0 & 7/2 & 2.5 \end{array} \middle\vert \begin{array}{c} 1\\0.5\\4\end{array}\right) \xrightarrow{R3\leftarrow R3 - R2}
\left( \begin{array}{ccc}
2 & -1 & 3 \\
0 & 7/2 & 0.5 \\
0 & 0 & 2 \end{array} \middle\vert \begin{array}{c} 1\\0.5\\3.5\end{array}\right)\)
So in row echelon form, we have no solution if we have some left row 0, but its right entry is not zero.
We have infinite number of solutions if some left row is zero and its right entry is also zero. From this, we can conclude that this system of equations has a unique solution
Q.49. What are the eigenvalues of the following 2*2 matrix?
$$\left( \begin{array}{cc}
2 & -1\\
-4 & 5\end{array}\right)$$
(A) -1 and 1
(B) 1 and 6
(C) 2 and 5
(D) 4 and -1
Sol : To calculate eigenvalues of a matrix, we find its characteristic equation, and then solve it. The characteristic equation of a matrix A is given by : $$ |A - λI| = 0$$ So for given matrix, characteristic equation is : $$|A - λI| = \left\vert \begin{array}{cc} 2-λ & -1\\-4 & 5-λ\end{array}\right\vert = (2-λ)(5-λ) - 4 = λ^2-7λ + 6= 0$$ So we get λ=1 and 6, so eigenvalues are 1 and 6, so option (B) is correct.
Q.50. Let $G(x) = \frac{1}{(1-x)^2} = \sum\limits_{i=0}^\infty g(i)x^i$, where |x| < 1. What is g(i)?
(A) i
(B) i+1
(C) 2i
(D) $2^i$
Sol : $G(x) = \frac{1}{(1-x)^2} = (1-x)^{-2} = 1 + 2x + 3x^2 +\cdots$ (from binomial theorem). So we can immediately see that g(i) should be i+1. So option (B) is correct.
Q.51. Box P has 2 red balls and 3 blue balls and box Q has 3 red balls and 1 blue ball. A ball is selected as
follows: (i) select a box (ii) choose a ball from the selected box such that each ball in the box is
equally likely to be chosen. The probabilities of selecting boxes P and Q are 1/3 and 2/3 respectively.
Given that a ball selected in the above process is a red ball, the probability that it came from the box
P is:
(A) 4/19
(B) 5/19
(C) 2/9
(D) 19/30
Sol : This can be done by bayes theorem. So $$\text{P(boxP | red)} = \frac{\text{P(red | boxP)}*\text{P(boxP)}}{\text{P(red | boxP)}*\text{P(boxP)} + \text{P(red | boxQ)}*\text{P(boxQ)}} = \frac{2/5 * 1/3}{2/5*1/3 + 3/4*2/3} = \frac{2/15}{19/30} = 4/19$$ So option (A) is correct.
Q.52. A random bit string of length n is constructed by tossing a fair coin n times and setting a bit to 0 or 1
depending on outcomes head and tail, respectively. The probability that two such randomly
generated strings are not identical is:
(A) $\frac{1}{2^n}$
(B) $1 - \frac{1}{n}$
(C) $\frac{1}{n!}$
(D) $1 - \frac{1}{2^n}$
Sol : So 2 bit strings will be identical when same sequence of head and tail comes while generating the sequences.
Now P(not identical) = 1 - P(identical) = 1 - $\frac{1}{2^n}$, because in each trial, prob of head and tail is 1/2, and
we toss the coin n times. So option (D) is correct.