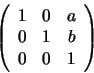How can we handle all this mathematically? -- Every point in an image represents a possible line of sight of an incoming light ray: any 3D point along the ray projects to the same image point, so only the direction of the ray is relevant, not the distance of the point along it. In vision we need to represent this ``celestial'' or ``visual sphere'' of incoming ray directions. One way to do this is by their two image (e.g. pixel) coordinates (x,y). Another is by arbitrarily choosing some 3D point along each ray to represent the ray's direction. In this case we need three ``homogeneous coordinates'' instead of two ``inhomogeneous'' ones to represent each ray. This seems inefficient, but it has the significant advantage of making the image projection process much easier to deal with.
In detail, suppose that the camera is at the origin (0,0,0). The ray
represented by ``homogeneous coordinates'' (X,Y,T) is that passing
through the 3D point (X,Y,T). The 3D point
![]() also lies on
(represents) the same ray, so we have the rule that rescaling
homogeneous coordinates makes no difference:
also lies on
(represents) the same ray, so we have the rule that rescaling
homogeneous coordinates makes no difference:
But what happens when T=0? -- (X,Y,0) is a valid 3D point that
defines a perfectly normal optical ray, but this ray does not
correspond to any finite pixel: it is parallel to the plane T=1 and
so has no finite intersection with it. Such rays or homogeneous
vectors can no longer be interpreted as finite points of the standard
2D plane. However, they can be viewed as additional ``ideal points''
or limits as (x,y) recedes to infinity in a certain direction:
Line coordinates: The planar line with equation
ax + by +c = 0is represented in homogeneous coordinates by the homogeneous equation
![]() .
If the line vector (a,b,c)is (0,0,1) we get the special ``line'' T=0 which contains only
ideal points and is called the line at infinity. Note that lines
are represented homogeneously as 3 component vectors, just as points
are. This is the first sign of a deep and powerful projective
duality between points and lines.
.
If the line vector (a,b,c)is (0,0,1) we get the special ``line'' T=0 which contains only
ideal points and is called the line at infinity. Note that lines
are represented homogeneously as 3 component vectors, just as points
are. This is the first sign of a deep and powerful projective
duality between points and lines.
Now consider an algebraic curve. The standard hyperbola has equation
xy = 1. Substitute
![]() and multiply
out to get
XY = T2. This is homogeneous of degree 2. In fact, in
homogeneous coordinates, any polynomial can be re-expressed as a
homogeneous one. Notice that
and multiply
out to get
XY = T2. This is homogeneous of degree 2. In fact, in
homogeneous coordinates, any polynomial can be re-expressed as a
homogeneous one. Notice that
![]() and
and
![]() are
valid solutions of
XY = T2: the homogeneous hyperbola crosses the
are
valid solutions of
XY = T2: the homogeneous hyperbola crosses the
![]() axis smoothly at
axis smoothly at ![]() and the
and the ![]() axis smoothly
at
axis smoothly
at ![]() ,
and comes back on the other side (see
fig. 1.2).
,
and comes back on the other side (see
fig. 1.2).