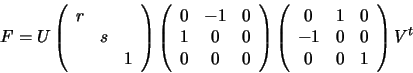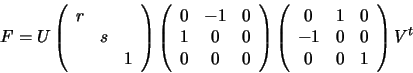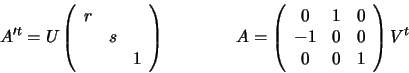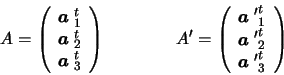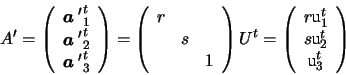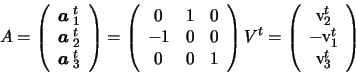


Next: Bibliography
Up: Self Calibration
Previous: Derivation of Kruppa's Equations
To derive explicit expressions for the matrices D and D' in terms
of the fundamental matrix F, let us reconsider the above argument.
Let F=UWVt be the Singular Value Decomposition of F. Here, Uand V are orthogonal, and W is a diagonal matrix with diagonal
values r, s, 0. We can write this as follows:
Define
Hence,
F = A'tF'A with A,A' non-singular and F' having the
desired canonical form. Applying the transformations
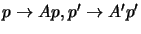 and
and
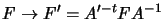 ,
we see that p'Fp is unchanged
and F becomes canonical, so A,A' are the required rectifying
transformations. These transformations take
,
we see that p'Fp is unchanged
and F becomes canonical, so A,A' are the required rectifying
transformations. These transformations take 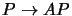 ,
,
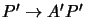 and hence
and hence 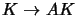 ,
,
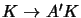 ,
and hence the DIAC C=KKt becomes
respectively D=ACAt and
D'=A'CA't.
,
and hence the DIAC C=KKt becomes
respectively D=ACAt and
D'=A'CA't.
Now explicitly compute the dij in order to use equation
(5.5). Decompose A and A' by rows:
Then,
D= ACAt implies
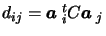 ,
and we
have the following explicit form for the Kruppa equations:
,
and we
have the following explicit form for the Kruppa equations:
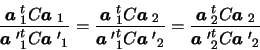 |
(5.6) |
We can write these equations directly in terms of the SVD of the
fundamental matrix.
where
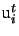 is the i-th column of U. And
is the i-th column of U. And
where
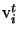 is the i-th column of V. From
(5.6) we obtain
is the i-th column of V. From
(5.6) we obtain
Our problem has five degrees of freedom. Each pair of images provides
two independent constraints. From three images we can form three pairs
which provide three pairs of constraints. This is enough to solve for
all the variables in C. However, note that all of the equations are
multivariable quadratics in the coefficients of C. This makes the
problem quite painful to solve in practise.
The difficulty of such purely algebraic approaches explains why
alternative approaches have been explored for self calibration.
[10] provides one such alternative. In any case, an
algebraic solution can only ever provide the essential first step for
a more refined bundle adjustment (error minimization) process.



Next: Bibliography
Up: Self Calibration
Previous: Derivation of Kruppa's Equations
Bill Triggs
1998-11-13