


Next: Harmonic Ratios and Involutions
Up: Some Standard Cross Ratios
Previous: Projective Bases for the
A pencil of planes in
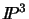 is a family of planes having a
common line of intersection. The cross ratio of four planes
is a family of planes having a
common line of intersection. The cross ratio of four planes 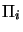 of a pencil is the same as the cross ratio of the lines li of
intersection of the planes with fifth, transversal plane (see
fig. 3.3).
of a pencil is the same as the cross ratio of the lines li of
intersection of the planes with fifth, transversal plane (see
fig. 3.3).
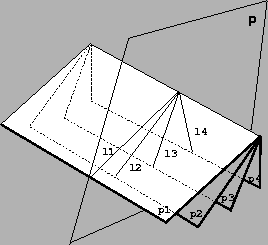
Figure 3.3:
A pencil of planes
 |
Once again, different transversal planes give the same cross ratio as
the figures they give are projectively equivalent. The Möbius formula
also extends to this case: let P, Q be any two distinct points on the
axis of the plane pencil, and
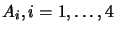 be points lying on
each plane
be points lying on
each plane 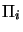 (not on the axis), then
(not on the axis), then
where
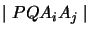 stands for a
stands for a 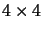 determinant of
4-component column vectors.
determinant of
4-component column vectors.
Bill Triggs
1998-11-13
![]() is a family of planes having a
common line of intersection. The cross ratio of four planes
is a family of planes having a
common line of intersection. The cross ratio of four planes ![]() of a pencil is the same as the cross ratio of the lines li of
intersection of the planes with fifth, transversal plane (see
fig. 3.3).
of a pencil is the same as the cross ratio of the lines li of
intersection of the planes with fifth, transversal plane (see
fig. 3.3).