Exercise 3.4
:
In an image, we see three equally spaced trees in a line. Explain how
the position of a fourth tree in the sequence can be predicted. If the
first tree lies at
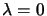
on the image line, the second lies at 1and the third at
c, what is the image coordinate of the fourth tree?