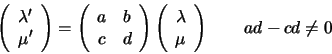Let
![]() be any four points on this line. Their cross
ratio
be any four points on this line. Their cross
ratio
![]() is defined to be:
is defined to be:
Theorem: The cross ratio does not depend on the choice of basis M and N on the line. If H is a collineation, then
See [23] for detailed proofs. In fact, invariance under
collineations need only be verified on the projective line
![]() :
: