Let
![]() and
and
![]() be homogeneous
representatives for two distinct points in the plane (i.e. M and
N are linearly independent 3-vectors:
be homogeneous
representatives for two distinct points in the plane (i.e. M and
N are linearly independent 3-vectors:
![]() ). Let
L=(a,b,c) be a the dual coordinates of a line (hyperplane) in the
plane. By the definition of a hyperplane, M lies on L if and only
if the dot product
). Let
L=(a,b,c) be a the dual coordinates of a line (hyperplane) in the
plane. By the definition of a hyperplane, M lies on L if and only
if the dot product ![]() vanishes, i.e. if and only if the
3-vector L is orthogonal to the 3-vector M. The line MN through
M and N must be represented by a 3-vector L orthogonal to both Mand N, and hence proportional to the cross product
vanishes, i.e. if and only if the
3-vector L is orthogonal to the 3-vector M. The line MN through
M and N must be represented by a 3-vector L orthogonal to both Mand N, and hence proportional to the cross product ![]() :
:
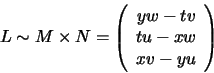
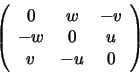
Another way to characterize the line MN is as the set of points
![]() for arbitrary
for arbitrary
![]() .
Evidently
.
Evidently
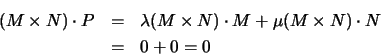
Dually, if L and L' are two lines defined by their dual coordinates,
then
![]() is some other line through the intersection
X of L and L' (since
is some other line through the intersection
X of L and L' (since
![]() implies
implies
![]() ). As
). As
![]() varies, this line traces out the
entire pencil of lines through X. By duality,
varies, this line traces out the
entire pencil of lines through X. By duality,
![]() .
.
One further way to approach lines is to recall that if M, N and Pare collinear, each point is a linear combination of the two others. In
particular, the ![]() determinant |MNP| vanishes. If M and Nare fixed, this provides us with a linear constraint that P must
satisfy if it is to lie on the line:
determinant |MNP| vanishes. If M and Nare fixed, this provides us with a linear constraint that P must
satisfy if it is to lie on the line:
![]() .
.