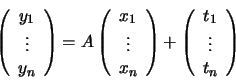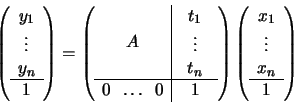


Next: Camera calibration:
Up: Projective Mappings
Previous: Projective Mappings
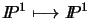 .
The general case of a collineation
is:
.
The general case of a collineation
is:
with
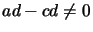 .
Provided
.
Provided 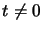 and
and
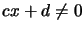 ,
this can
be rewritten in inhomogeneous affine coordinates as:
,
this can
be rewritten in inhomogeneous affine coordinates as:
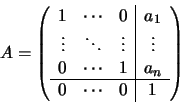
Property: A translation in affine space corresponds to a collineation leaving each
point at infinity invariant.
Proof: The translation
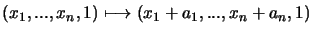 can be represented by the matrix:
can be represented by the matrix:
Obviously
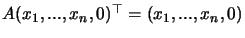 .
.

More generally, any affine transformation is a collineation, because it can be
decomposed into a linear mapping and a translation:
In homogeneous coordinates, this becomes:
Exercise 2.1
:
Prove that a collineation is an affine transformation if and only if it
maps the hyperplane at infinity xn+1=0 into itself (i.e. all
points at infinity are mapped onto points at infinity).
Bill Triggs
1998-11-13
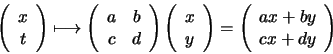
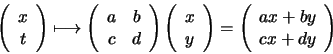
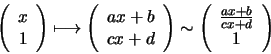
![]() can be represented by the matrix:
can be represented by the matrix: