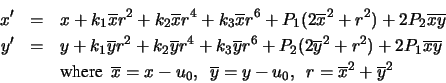
Perspective (i.e. pinhole) projection is an idealized mathematical model of the behaviour of real cameras. How good is this model? -- There are two aspects to this: extrinsic and intrinsic.
Light entering a camera has to pass through a complex lens system. However, lenses are designed to mimic point-like elements (pinholes), and in any case the camera and lens is usually negligibly small compared to the viewed region. Hence, in most practical situations the camera is ``effectively point-like'' and rather accurately satisfies the extrinsic perspective assumptions: (i) for each pixel, the set of 3D points projecting to the pixel (i.e. whose possibly-blurred images are centered on the pixel) is a straight line in 3D space; and (ii) all of the lines meet at a single 3D point (the optical center).
On the other hand, practical lens systems are nonlinear and can easily introduce significant distortions in the intrinsic perspective mapping from external optical rays to internal pixel coordinates. This sort of distortion can be corrected by a nonlinear deformation of the image-plane coordinates.
There are several ways to do this. One method, well known in the
photogrammetry and vision communities, is to explicitly model the
radial and decentering distortion (see [24]): if the
center of the image is
(u0, v0), the new coordinates (x',
y') of the corrected point are given by
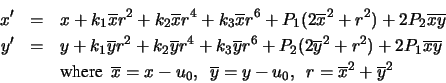
A more general method that does not require knowledge of the principal point and makes no assumptions about the symmetry of the distortion is based on a fundamental result in projective geometry:
Theorem: In real projective geometry, a mapping is projective if and only if it maps lines onto either lines or points.
Hence, to correct for distortion, all we need to do is to observe
straight lines in the world and deform the image to make their images
straight. Experiments described in [2] show accuracies of
up to
![]() of the image for standard off-the-shelf CCD
cameras. Figure 1.4 illustrates the process: line
intersections are accurately detected in the image, four of them are
selected to define a projective basis for the plane, and the others
are re-expressed in this frame and perturbed so that they are
accurately aligned. The resulting distortion corrections are then
interpolated across the whole image.
of the image for standard off-the-shelf CCD
cameras. Figure 1.4 illustrates the process: line
intersections are accurately detected in the image, four of them are
selected to define a projective basis for the plane, and the others
are re-expressed in this frame and perturbed so that they are
accurately aligned. The resulting distortion corrections are then
interpolated across the whole image.