Next: Video compression Up: Some Applications Previous: Novel view generation using
Given a set of input images such as:
![\includegraphics[width=0.4\textwidth]{00.eps}](img143.png)
![\includegraphics[width=0.4\textwidth]{14.eps}](img144.png)
![\includegraphics[width=0.4\textwidth]{04.eps}](img145.png)
![\includegraphics[width=0.4\textwidth]{09.eps}](img146.png)
consider the problem of genrating a novel view.
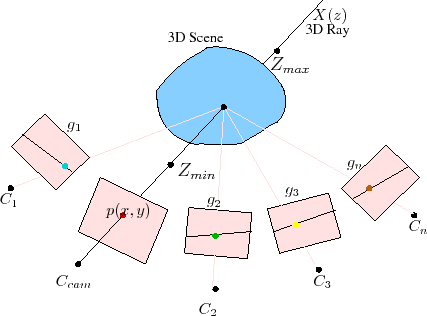
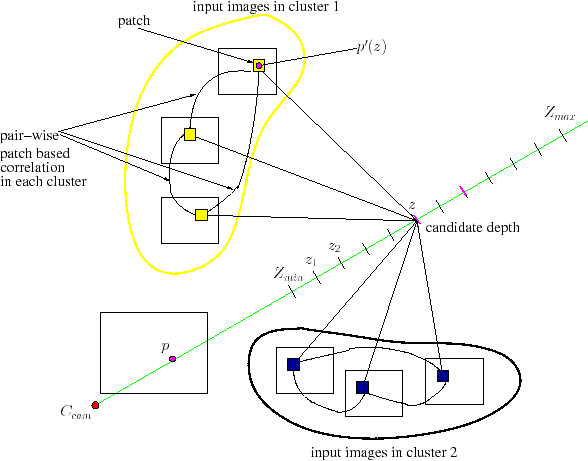
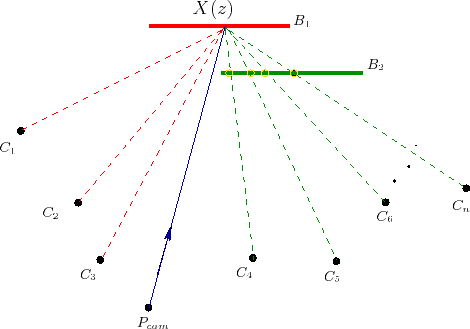
| (2) |
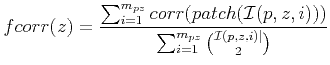 |
(3) |
![\includegraphics[width=0.4\textwidth]{00.eps}](img143.png) |
![\includegraphics[width=0.4\textwidth]{depth40.eps}](img170.png) |
| (a) | (b) |
![\includegraphics[width=0.4\textwidth]{occlusion40.eps}](img171.png) |
![\includegraphics[width=0.4\textwidth]{color40.eps}](img172.png) |
| (c) | (d) |
![\includegraphics[width=0.4\textwidth]{NovelViewYellowFlower_2010_340270.eps}](img173.png)
![\includegraphics[width=0.4\textwidth]{Diff_NovelView05_YellowFlower_2010_340270.eps}](img174.png)
Subhashis Banerjee 2008-01-21