- Given the two cameras 1 and 2, we have the camera equations:
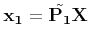
and
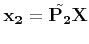
- The optical center projects as
- Writing
where 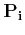 is
is
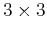 non-singular we have that
non-singular we have that
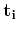 is the optical center.
is the optical center.
- The epipole
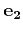 in the second image is the projection of the
optical center of the first image:
in the second image is the projection of the
optical center of the first image:
- The projection of point on infinity along the optical ray
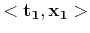 on to the second image is given by:
on to the second image is given by:
- The epipolar line
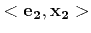 is given by the
cross product
is given by the
cross product
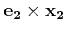 .
.
- If
![$ \left[ {\bf e_2} \right]_{\times}$](img16.png) is the
is the
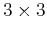 antisymmetric matrix representing cross product with
antisymmetric matrix representing cross product with 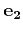 ,
then we have that the epipolar line is given by
,
then we have that the epipolar line is given by
- Any point
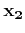 on this epipolar line satisfies
on this epipolar line satisfies
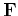 is called the fundamental matrix. It is of rank 2 and
can be computed from 8 point correspondences.
is called the fundamental matrix. It is of rank 2 and
can be computed from 8 point correspondences.
- Clearly
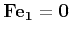 (degenerate epipolar line) and
(degenerate epipolar line) and
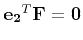 . The epipoles are
obtained as the null spaces of
. The epipoles are
obtained as the null spaces of 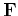 .
.
Subhashis Banerjee
2008-01-21
![$\displaystyle \left[ {\bf P_i} \mid -{\bf P_i}{\bf t_i} \right]
\left[ \begin{array}{c} {\bf t_i} \\ 1 \end{array} \right] = {\bf0}
$](img9.png)
![$\displaystyle {\bf e_2} = \tilde{\bf P_2} \left[ \begin{array}{c} {\bf t_1} \\ 1 \end{array} \right]
$](img11.png)