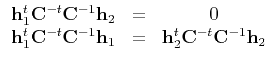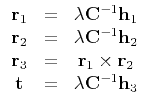- Camera calibration from a single plane at few (at least three, two skew is ignored) orientations.
- Without loss of generality, assume that the model plane is on
 .
.
- Then, for points on the model plane
- Thus, a model point
 and its image
and its image 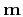 are related by
a homography
are related by
a homography  , where
, where
with
- From
using the fact that 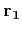 and
and 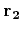 are orthonormal,
we obtain the relationships
are orthonormal,
we obtain the relationships
- Each such homography provides two constraints on the camera intrinsics
(image of the absolute conic). Three independent orientations
are sufficient to solve for camera internals linearly. Two are
sufficient if the skew is ignored.
- Once the camera internals matrix
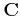 is known, the externals
can be readily obtained.
is known, the externals
can be readily obtained.
with
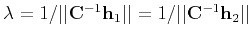 .
Of course, the computed matrix
.
Of course, the computed matrix
![$ {\bf R} = \left[ {\bf r}_1\;\; {\bf r}_2 \;\; {\bf r}_3 \right]$](img482.png) does not, in general, satisfy the properties of a
rotation matrix. The orthonormality properties can be enforced in manned similar
to the one described in Tsai's.
does not, in general, satisfy the properties of a
rotation matrix. The orthonormality properties can be enforced in manned similar
to the one described in Tsai's.
- The method can be extended to also obtain the radial lens distortion
parameters.
Subhashis Banerjee
2008-01-20
![$\displaystyle s \left[
\begin{array}{c} u \\ v \\ 1 \end{array}\right]
=
{\bf C...
...f t}
\end{array}\right]
\left[
\begin{array}{c} X \\ Y \\ 1 \end{array}\right]
$](img475.png)