Determining calibration from vanishing points and lines

• Let ${\bf v}_1$ and ${\bf v}_2$ be the vanishing points of two lines in the image. If $\theta$ is the angle between the two scene lines, we have
  $$\begin{array}{lll} \cos{\theta} & = & \frac{{{\bf v}_1}^T {\bf\... ...f\omega} {\bf v}_1} \sqrt{{{\bf v}_2}^T {\bf\omega} {\bf v}_2}} \\ \end{array}$$

• If $\theta$ is known the above equation gives a quadratic constraint on the entries of ${\bf\omega}$ .
• If it is known that the scene lines are orthogonal ( $\theta = 90$ ), then we have a linear constraint
  $${{\bf v}_1}^T {\bf\omega} {\bf v}_2 = 0$$
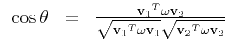
  Thus, given five pairs of perpendicular lines, one can solve for the entries of ${\bf\omega}$ .
• The vanishing point ${\bf v}$ of the normal direction to a plane is obtained from the plane vanishing line as
  $${\bf l} = {\bf C}^{-T} {\bf n} = {\bf C}^{-T} {\bf C}^{-1}{\bf v} = {\bf\omega}{\bf v}$$
  A common example is a vertical direction and a horizontal plane.
• Writing the above as ${\bf l} \times {\bf\omega}{\bf v} = {\bf0}$ removes the homogeneous scaling factor and results in three homogeneous equations linear in the entries of ${\bf\omega}$ .
• Given a sufficient number of such constraints ${\bf\omega}$ can be computed and ${\bf C}$ follows.
• The following can be verified by direct computation:
  1. If $s = {\bf C}_{12} = 0$ ( no skew) then $\omega_{12} = \omega_{21} = 0$ .
  2. If, in addition, $\alpha_x = \alpha_y = {\bf C}_{11} = {\bf C}_{22}$ then $\omega_{11} = \omega_{22}$
• Suppose it is known that the camera has zero skew and that the pixels are square (or the aspect ratio is known) the ${\bf\omega}$ and ${\bf C}$ can be computed from an orthogonal triad of directions.