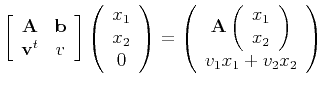The affine subgroup

In an affine space ${\cal A}^n$ an affine transformation defines a correspondence ${\bf X} \leftrightarrow {\bf X'}$ given by:

$${\bf X'} = {\bf A} {\bf X} + {\bf b}$$

where ${\bf X}$ , ${\bf X'}$ and ${\bf b}$ are $n$ -vectors, and ${\bf A}$ is an $n \times n$ matrix.

Clearly this is a subgroup of the projective group. Its projective representation is

$${\bf T} = \left[ \begin{array}{cc} {\bf C} & {\bf c} \\ {\bf0}_n^T & t_{33} \end{array}\right]$$

where ${\bf A} = \frac{1}{t_{33}}{\bf C}$ and ${\bf b} = \frac{1}{t_{33}}{\bf c}$ .

The affine subgroup preserves the hyperplane at infinity.

$$\left[ \begin{array}{cc} {\bf A} & {\bf b} \\ {\bf0}^t & 1 \end{... ...\left( \begin{array}{c} x_1 \\ x_2 \end{array}\right) \\ 0 \end{array}\right)$$

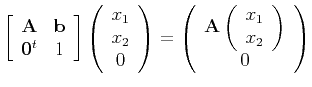
On the other hand, a general projective transformation moves points at infinity to a finite point.

$$\left[ \begin{array}{cc} {\bf A} & {\bf b} \\ {\bf v}^t & v \end... ...ray}{c} x_1 \\ x_2 \end{array}\right) \\ v_1 x_1 + v_2 x_2 \end{array}\right)$$