


Next: Numbering computable functions
Up: MFCS: Problem set 1
Previous: URM programs
Do the following without writing any programs.
- Show that for every
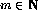 the following functions are
computable:
the following functions are
computable:
-
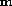 (recall that
(recall that 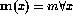 )
) - mx
- Suppose that f(x,y) is a computable function and
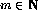 . Show that
the function
. Show that
the function 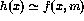 is computable.
is computable. - Suppose that the function g(x) is a total computable function.
Show that the predicate
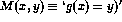 is decidable.
is decidable. - Show that the following functions are computable:
- Any polynomial function
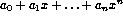 where
where 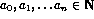
-
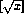
- LCM(x,y)
- HCF(x,y)
- the number of prime divisors of x
- the number of positive integers less that x
which are relatively prime to x. (x and y are
relatively prime if HCF(x,y) = 1.)
- f(0) = 1; f(1) = 2; f(n+2) = f(n) + f(n+1). (f(n)
is the
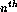 Fibonacci number.)
Fibonacci number.)
(Hint: show that the function 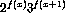 is computable using recursion.)
is computable using recursion.)
- Show that the following are decidable:
- x is odd
- x is a power of a prime number
- x is a perfect cube
- Suppose that f(x) is a total injective computable function. Prove that
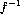 is computable.
is computable. - Suppose that p(x) is a polynomial with integer coefficients. Show
that the function f(a) = least non-negative integral root of
p(x) -a where
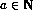 is computable (f(a) is undefined if there
is no such root.)
is computable (f(a) is undefined if there
is no such root.) - Show that the function
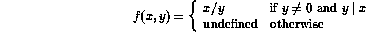
is computable.
Subhashis Banerjee
Fri Sep 5 15:54:45 IST 1997
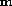 (recall that
(recall that 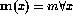 )
)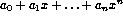 where
where 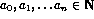
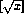
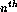 Fibonacci number.)
Fibonacci number.) 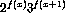 is computable using recursion.)
is computable using recursion.)
![]()