


Next: About this document
MFCS (CS755N) Minor II October 1, 1997
Maximum marks : 50
NOTE:
- Notations are standard (as done in the class).
- You may use any result done in the class.
- Q1 and Q2 are of 10 marks each. Q3 and Q4 are of 15 marks each.
-
- Use a direct diagonal construction to show that the
problem `
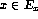 is undecidable.
is undecidable. - Show that the problem `
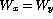 ' is undecidable by
reducing `
' is undecidable by
reducing ` 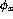 is total' to this problem.
is total' to this problem.
- Prove that a partial function f is computable if and only if
the predicate
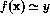 is partially decidable.
is partially decidable. - Suppose that f is a total computable function, A is a recursive
set and B is a recursively enumerable set. Show that
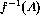 is recursive and that f(A), f(B) and
is recursive and that f(A), f(B) and 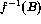 are recursively
enumerable but not necessarily recursive. What extra information can
be obtained about these sets if f is a bijection?
are recursively
enumerable but not necessarily recursive. What extra information can
be obtained about these sets if f is a bijection? - Use Rice-Shapiro's theorem to show that the following problems are not
partially decidable:
- `
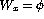 '
' - `
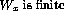 '
' - `
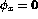 '
'
Subhashis Banerjee
Thu Oct 2 10:40:07 IST 1997
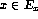 is undecidable.
is undecidable.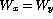 ' is undecidable by
reducing `
' is undecidable by
reducing ` 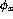 is total' to this problem.
is total' to this problem.
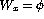 '
'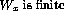 '
'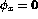 '
'