- a set
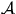 of N airports, and for each airport
of N airports, and for each airport
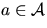 , a minimum connect time c(a)
, a minimum connect time c(a)
- A set
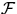 of M flights, and the following information,
for each flight
of M flights, and the following information,
for each flight 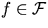 :
: - Origin airport
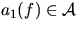
- Destination airport
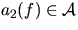
- Departure time t1(f)
- Arrival time t2(f)
- Origin airport
Given airports a and b, and a time t, find a sequence of flights that allows one to arrive at the earliest possible time in b when departing from a at or after time t. Minimum connecting time at intermediate airports should be observed.