


Next: About this document ...
CS130N Problem set 7: Basic graph traversal
- 1.
- Describe the details of an O(n+m) time algorithm for computing
all connected components of an undirected Graph G with m vertices
and n edges.
- 2.
- Let T be a spanning tree produced by the DFS of a connected undirected
graph G. Argue why every edge of G, not in T, goes from a vertex
v in T to one of its ancestors, that is, it is a back edge.
- 3.
- Show that, if T is a BFS tree produced for a connected graph G, then,
for each vertex v at level i, the path of T between s and v
has i edges, and any other path of G between s and v has at
least i edges.
- 4.
- Given a tree T of n nodes the diameter of T is the length of
a longest path between two nodes of T. Give an efficient algorithm
to compute the diameter of T.
- 5.
- An independent set of an undirected graph G = (V,E) is a subset
I of V such that no two vertices in I are adjacent. That is,
if
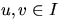 then
then 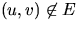 . A maximal independent set M
is an independent set such that, if we were to add any additional
vertex to M, then it would not be independent any more. Prove that
every graph has a maximal independent set. Give an efficient
algorithm to compute the maximal independent set of a given graph G.
. A maximal independent set M
is an independent set such that, if we were to add any additional
vertex to M, then it would not be independent any more. Prove that
every graph has a maximal independent set. Give an efficient
algorithm to compute the maximal independent set of a given graph G.
- 6.
- An Euler tour of a directed graph G with n vertices and
m edges is a cycle that traverses each edge of G exactly once
according to its direction. Such a tour always exists if the
in-degree equals the out-degree for every vertex in G. Describe
an O(n+m) time algorithm for finding a Euler tour of such a
graph G.
- 7.
- Let G be an undirected graph with n vertices and m edges.
Describe an O(n+m) time algorithm for traversing each edge
of G exactly once in each direction.
- 8.
- A node p of a directed graph G = (V,E) is called a sink if
for every node
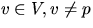 the edge (v,p) exists, whereas
the edge (p,v) does not exist. Describe an algorithm that can
detect the presence of a sink in G in O(n) time (n is the
number of vertices). Your algorithm should accept the graph
represented by its adjacency matrix. (Notice that the running
time O(n) for this problem is remarkable given that the
instance takes a space in
the edge (v,p) exists, whereas
the edge (p,v) does not exist. Describe an algorithm that can
detect the presence of a sink in G in O(n) time (n is the
number of vertices). Your algorithm should accept the graph
represented by its adjacency matrix. (Notice that the running
time O(n) for this problem is remarkable given that the
instance takes a space in 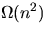 merely to write down).
merely to write down).



Next: About this document ...
Subhashis Banerjee
4/24/2001