


Next: About this document ...
CS130N Problem set 3: Some Data structures + Algorithms
- Sparse polynomials:
- A polynomial
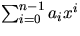 is called dense if
almost all the coefficients are non-zero. If the number
of nonzero coefficients is much smaller than the largest degree
then the polynomial is sparse. The most natural
representation of a sparse polynomial is as a sorted list
of pairs (ai,ji) of nonzero coefficients and the
corresponding powers of x. While algorithms for
addition and multiplication of dense polynomials can be
similar to those for big numbers, sparse polynomials
need to be handled differently (why?). Develop algorithms for
computing addition, multiplication and division (reciprocal)
of sparse polynomials.
is called dense if
almost all the coefficients are non-zero. If the number
of nonzero coefficients is much smaller than the largest degree
then the polynomial is sparse. The most natural
representation of a sparse polynomial is as a sorted list
of pairs (ai,ji) of nonzero coefficients and the
corresponding powers of x. While algorithms for
addition and multiplication of dense polynomials can be
similar to those for big numbers, sparse polynomials
need to be handled differently (why?). Develop algorithms for
computing addition, multiplication and division (reciprocal)
of sparse polynomials.
- Sparse matrices:
- A matrix is sparse if most elements of the matrix are
zero. We might store a large sparse matrix (to save space)
as a list of triples (i,j,value) where (i,j) is a
position and value is a non-zero value. We may represent
the list in an array A[t,3], where t is an upper bound
on the number of non-zero elements. Further, we may
maintain the list sorted so that the row numbers are
increasing and within a row the column numbers are increasing.
Design algorithms to i) transpose a sparse matrix ii) add
two sparse matrices and iii) multiply two sparse matrices.
- Knight's tour:
- Consider a
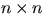 chess board
with a knight placed on a square of initial
position (x0,y0). Develop an algorithm to determine
a covering of the entire board, if there exists one, i.e.,
to compute a tour of n2 - 1 moves such that every
field of the board is visited exactly once.
chess board
with a knight placed on a square of initial
position (x0,y0). Develop an algorithm to determine
a covering of the entire board, if there exists one, i.e.,
to compute a tour of n2 - 1 moves such that every
field of the board is visited exactly once.
- Stable marriage:
- Consider a set A of men and
a set B of women. Each man and each woman has stated
distinct preferences for their partners. If n couples
are chosen such that there exists a man and woman who
would both prefer each other to their actual marriage
partners then the pairing is said to be unstable
(for obvious reasons). If no such pair exists, then
the pairing is stable. Develop an algorithm
to compute all stable marriage assignments.
- FFT multiplication:
- Study the Fast Fourier Transform algorithm (tutors please
help) and figure out how it can be used for efficient
multiplication of big numbers.



Next: About this document ...
Subhashis Banerjee
1/23/2001