


Next: About this document ...
Data Structures (CS130N) Major May 2, 2001
Name: Entry: Grp:
Note:
Maximum marks: 120 (a mark a minute). Answer only in the space provided.
5 pages in all. All questions carry equal marks. Q7 is bonus and
will be considered only if the others have been answered.
- 1.
- Show that a binary tree can be uniquely reconstructed from its inorder
and preorder traversal sequences. What is the time complexity?
- 2.
- Let S be a set of distinct binary strings whose lengths
sum up to n. Show how to sort S in
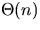 time.
Note that since the input parameter n is unknown you
cannot use a static structure like an array.
time.
Note that since the input parameter n is unknown you
cannot use a static structure like an array.
- 3.
- Consider a simple list based implementation of the abstract
data type ClearableStack which supports the usual
operations create, push, pop, isempty and an additional
clearstack operation which clears a stack containing
n elements in
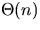 time. Show that a series of n
of the above operations on an initially empty ClearableStack
takes O(n) time.
time. Show that a series of n
of the above operations on an initially empty ClearableStack
takes O(n) time.
- 4.
- An Euler tour of a directed graph G with n vertices
and m edges is a cycle that traverses each edge of G exactly
once according to its direction. Such a tour always exists if the
in-degree equals the out-degree of each vertex in G. Give an
efficient algorithm for finding a Euler tour in such a graph G.
- 5.
- Consider the following algorithm for finding the Euclidean
minimum spanning tree of a graph:
``Sort the points on their x coordinates, then find the
minimum spanning trees of the first half and the second
half, then find the shortest edge that connects them.''
Is the algorithm correct? If yes, give a proof and run time
analysis; if not, give a proof that it doesn't work.
- 6.
- Consider the following greedy strategy for finding a shortest
path from a vertex start to a vertex goal in a
given connected graph:
- (a)
- Initialize path to start.
- (b)
- Initialize VisitedVertices to
 .
. - (c)
- If start = goal, return path and exit.
- (d)
- Find the edge (start,v) of minimum weight such
that v is adjacent to start and
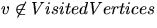 .
. - (e)
- Add v to path.
- (f)
- Add v to VisitedVertices.
- (g)
- Set start = v and go to step 3.
Is the algorithm correct? If yes, give a proof and run time
analysis; if not, give a proof that it doesn't work.
- 7.
- Bonus:
Consider the Bellman-Ford algorithm for finding the
single source shortest path in a connected digraph:
![\begin{displaymath}
\begin{array}
{l}
\mbox{Let $n$\space be the number of vert...
...\mbox{ $D[z] \leftarrow D[u] + w(u,z)$\space }
\end{array}
\end{displaymath}](img4.gif)
Prove the following:
If after performing the above computation there is an edge (u,z)
that can be relaxed (that is D[u] + w(u,z) < D[z]), then the
graph contains a negative weight cycle. Otherwise
D[u] = d(v,u), the length of the shortest path from v to u
for all u in the graph even if there are negative weights.



Next: About this document ...
Subhashis Banerjee
5/2/2001
 .
. 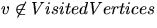 .
. ![\begin{displaymath}
\begin{array}
{l}
\mbox{Let $n$\space be the number of vert...
...\mbox{ $D[z] \leftarrow D[u] + w(u,z)$\space }
\end{array}
\end{displaymath}](img4.gif)