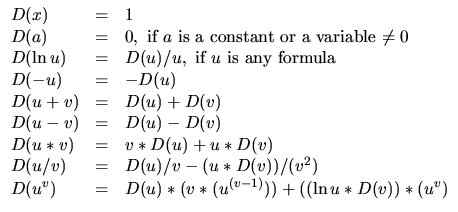
- a string in fully parenthesized infix form
- a string in postfix form
- fully parenthesized infix:
((3*ln(x+1))-(~a/(x^2.0)))
- postfix:
3.0 x 1 + ln * a ~ x 2 ^ / -
- opearators to be supported are:
+ - * / ^ ~ ln (usual meanings) - numbers may be written as either 3 or 3.0
- there will be no blanks in the infix input string. The tokens in the postfix input string will be separated by exactly one blank.
- variables names may contain arbitrary number of characters and numerals but must start with an alphabet.
In particular, you will get bonus if you can provide methods for checking equality of expressions. This will require you to reduce your expressions to a suitable normal form.