MATHEMATICAL PROGRAMMING (CS 856/450)

Assignment 1 :

1.

Devise a linear program formulation for the ATM Cash Problem discussed in the class.

2.

Show that the General, Canonical and Standard Formulations of Linear Programs are equivalent.

3.

Show the equivalence of the Canonical Form to a polyhedron formed by the intersection of m halfspaces.

4.

Prove that degenerate basic feasible solutions which are same in non-zero components correspond to the same vertex.

5.

Show: If no adjacent BFS of a BFS B has cost less than that of B then B is optimal.

6.

Supoose b₁ and b₂ are two BFS's which are not adjacent to each other and C1 and C2 are the columns corresponding to the BFS's b₁ and b₂ then there exists another basis in $C1 \cup C2$.

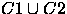7.

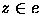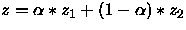Prove that if e is an edge of a polyhedron and $z \in e$, i.e $z= \alpha *z_1 + (1- \alpha ) * z_2$,then z₁,z₂ belong to e.

8.

Resolve the assumption b>=0 in the derivation of Simplex Method.

9.

Prove that Bland's Rule which is

Use lowest numbered column for basis change and use lowest numbered row for determining 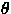$\theta$.

prevents cyclicity in the Simplex Method.

10.

Design Linear Programs which demonstrate the relationship possible between primal & dual from the set of properties of bounded feasiblity, unbounded feasibility and infeasibility.

11.

Analyze the worst case behaviour of the Simplex. This should include the time for pivoting also.