CSL102: Introduction to Computer Science
II semester 2004-05

Ordinary first order differential equations with initial values

Consider an ordinary differential equation of the form

$$y' = f(x, y), \hspace{3cm} y(x_0) = y_0$$ (1)

We need to solve this equation and obtain the value of the function $y(x)$ at some point $x_f$. For any value $x$ and a small step $\Delta x$ we have from the Taylor series expansion

$$y(x+\Delta x) = \Sigma_{i\geq 0} \frac{(\Delta x)^{i}}{i!} y^{(i)}(x)$$ (2)

where $y^{(i)}(x)$ denotes the $i$-th total derivative of $y(x)$ at the point $x$. By truncating the Taylor expansion upto some value $i=n$ we could get fairly close to the actual solution of equation (1). However, this requires being able to find derivatives upto order $n$. That is usually very difficult and time-consuming for arbitrary functions.

A fairly accurate method for obtaining numerical solutions to equation (1) is the Runge-Kutta method¹ and is used in most packages. In this method there is no need to calculate higher order derivatives.

Runge-Kutta Methods

We describe below the Runge-Kutta method of second order:

Let the interval $[x_0, x_f]$ be divided into steps of size $\Delta x = \displaystyle{\frac{x_f - x_0}{N}}$, for some appropriately chosen $N$. Assume we want to to compute $y_N = y(x_f)$ using a formula of the form of the form

$$y_{n+1} = y_n + aA_n + bB_n$$ (3)

which generates approximations $y_n$ to $y(x_0 + n \Delta x)$ for each value of $n = 0, 1, \ldots, N$ where

$$\begin{array}{lcl} A_n &=& (\Delta x)f(x_{n}, y_{n})\\ B_n &=& (\Delta x)f(x_n + \alpha\Delta x, y_n + \beta A_n) \end{array}$$

and $a$, $b$, $\alpha$ and $\beta$ are constants to be determined, so that (3) will agree with (2) for as high an order of terms as possible.

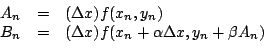
On expanding $y(x_{n+1})$ through the Taylor expansion we get

$$\begin{array}{lcl} y(x_{n+1}) &=& y(x_n) + \displaystyle{(\De... ..._{xy} +f_xf_y + f_y^2f)_n + {\cal O}((\Delta x)^4)} \end{array}$$

where the subscript $n$ means that all functions are evaluated at $(x_n, y_n)$.

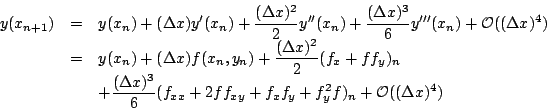
On the other hand using Taylor's exapansion for functions of two variables we get that

$$\begin{array}{lcl} \displaystyle{\frac{B_n}{\Delta x}} &=& f... ...c{\beta^2 A_n^2}{2}f_{yy} + {\cal O}((\Delta x)^3)} \end{array}$$

where all derivatives are evaluated at $(x_n, y_n)$.

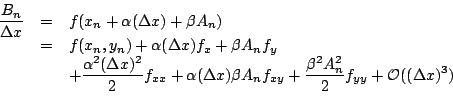
If we substitute this expression for $B_n$ into the formula (3) and use $A_n = (\Delta x)f(x_n, y_n)$, we find after rearranging the powers of $\Delta x$ that

$$\begin{array}{lcl} y_{n+1} &=& y_n + (a+b)(\Delta x)f + b(\D... ..._{xy} + \beta^2f^2f_{yy}) + {\cal O}((\Delta x)^4)} \end{array}$$

On comparing this with the previous Taylor expansion, we find that in order for the coefficients of $\Delta x$ and $(\Delta x)^2$ to match we must have

$$\begin{array}{lclcl} a &+& b &=& 1\\ b\alpha &=& b\beta &=& \frac{1}{2} \end{array}$$

since $y'(x_n) = f(x_n, y_n)$ and $y''(x_n) = f'(x_n, y_n) = (f_x + f_yy' = f_x + f_yf)_n$. Though there are many solutions to the above equations, the simplest are the following:

$$a=b=\frac{1}{2} \hspace{3cm} \alpha = \beta = 1$$

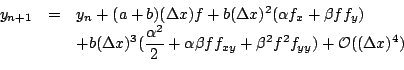
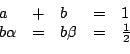
As one can see it is not necessary to compute any higher derivatives, yet it is possible to get an accuracy upto the second-order terms of the Taylor expansion. Hence this method is called Runge-Kutta of second order. An even more accurate method called the Runge-Kutta of fourth order involves computing four auxiliary quantities

$$\begin{array}{lcl} A_n &=& (\Delta x)f(x_{n}, y_{n})\\ B_n &... ...n}{2})}\\ D_n &=& (\Delta x)f(x_{n+1}, y_n + C_n) \end{array}$$

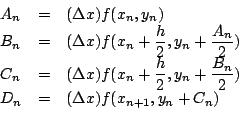
and using the formula

$$y_{n+1} = y_n +\frac{1}{6}(A_n + 2B_n + 2C_n + D_n)$$ (4)

This method can be shown to be accurate upto the fourth order terms of the Taylor expansion. However it is too complicated and tedious to explain and justify.

What you have to do

Develop a higher order function runge_kutta_4 which solves any ordinary initial value problem for a given parameter $x_f$ using the fourth order Runge-Kutta method (4). Give at least 5 examples of functions involving trigonometric functions, exponentials and polynomials and setup initial value problems and solve them for chosen values of $x_f$ and determine the extent to which the anlytical solutions match the numerical solutions. Note:

1. You are not allowed to change any of the names given in the signature. You are not even allowed to change upper-case letters to lower-case letters or vice-versa.
2. You may define any new functions you like in the structure besides those mentioned in the signature.
3. Your program should work with the given signature.
4. You need to think of the most efficient way of implementing the various functions given in the signature so that the function results satisfy their definitions and properties.
5. Since the evaluator is going to look at your source code before evaluating it, you must explain your algorithms in the form of ML comments, so that the evaluator can understand what you have implemented.
6. Do not add any more decorations or functions or user-interfaces in order to impress the evaluator of the program. Nobody is going to be impressed by it.
7. There is a serious penalty for copying. If it is felt that there is too much similarity in the code between any two persons, then both are going to be penalized equally. So please set permissions on your directories, so that others cannot copy your programs.