


Von Neumann And Morgenstern Utility Function
Vishrut Goyal and Anuj S. Saxena
In last lecture we discussed the St. Petersburg Paradox, where although the expected return from the game is infinity, only a few gamblers are willing to invest large amount of money. Now we take a simplified version of the above paradox.
Consider a player being given two options : Take Rs.10 for sure or Rs.70 with probability 0.5. In this case, the player is likely to go for the second option.
Now consider the case when Rs 10 and Rs.70 were replaced by Rs. 10 million and Rs.70 million respectively. In this case, the user is likely to go for the first option. Why is it so? Why people may not want to maximize their expected gain?
Let 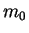 be the initial amount of money with the user. Let
be the initial amount of money with the user. Let 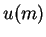 be a utility function representing the user's preference relation. The expected utility in each of the options in the cases discussed above is summarized below :
be a utility function representing the user's preference relation. The expected utility in each of the options in the cases discussed above is summarized below :
| |
Option 1 |
Option 2 |
|---|
| Case A |
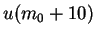 |
![$1/2[u(m_0) + u(m_0 + 70)]$](img4.png) |
|---|
| Case B |
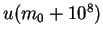 |
![$1/2[u(m_0) + u(m_0 + 7*10^8)]$](img6.png) |
|---|
Assume that the player has initially Rs. 10,000. i.e. 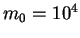 .
.
Consider the case when 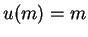 . Now the expected utilities are given in the following table :
. Now the expected utilities are given in the following table :
| |
Option 1 |
Option 2 |
|---|
| Case A |
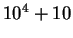 |
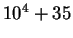 |
|---|
| Case B |
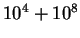 |
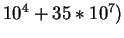 |
|---|
Here we see that the expected utility is more for option 2 in both the cases. Therefore players should prefer option 2 in both the cases
In earlier lecture we saw that if a utility function 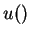 represents a preference relation R, then f(u()) also represents R, where f() is a monotonically increasing function. Therefore
represents a preference relation R, then f(u()) also represents R, where f() is a monotonically increasing function. Therefore
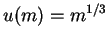 should represent the same preference relation as
should represent the same preference relation as 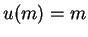 . If we assume
. If we assume
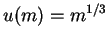 , then the expected utilities are given in the following table :
, then the expected utilities are given in the following table :
| |
Option 1 |
Option 2 |
|---|
| Case A |
![$10^{4/3}[1 + \frac{1}{3000}]$](img15.png) |
![$10^{4/3}[1 + \frac{3.5}{3000}]$](img16.png) |
|---|
| Case B |
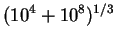 |
![$1/2[10^{4/3} + (10^4 + 7*10^8)^{1/3}]$](img18.png) |
|---|
Here we see that that expected utility is more for option 2 in case A and is more for option 1 in case B as one would generally expect in real life. Notice that
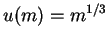 does not represent the same preference relation as
does not represent the same preference relation as 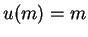 . This can be explained using Von Neumann and Morgenstern utility function.
. This can be explained using Von Neumann and Morgenstern utility function.
Let 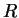 be a preference relation over a set of deterministic outcomes
be a preference relation over a set of deterministic outcomes 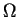 and
and
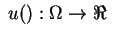 be a utility function representing
be a utility function representing 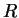 . If we have probabilistic outcomes, then the preference relation
. If we have probabilistic outcomes, then the preference relation 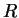 should be defined over probabilistic outcomes
should be defined over probabilistic outcomes
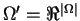 . Now the utility function has to be redefined so as to represent this new preference relation. Therefore, now
. Now the utility function has to be redefined so as to represent this new preference relation. Therefore, now
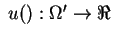 .
.
Notation : Let
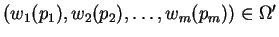 , where
, where 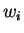 is
is 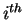 outcome in
outcome in 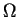 and
and 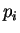 is the probability of occurrence of
is the probability of occurrence of 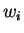 s.t.
s.t.
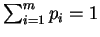 .
.
Von Neumannn and Morgenstern gave a set of rationality postulates, which define preference relation in probabilistic outcomes.
Consider any two outcomes (namely 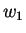 and
and 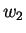 ) from the set
) from the set 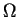 , with outcome
, with outcome 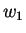 being preferred over outcome
being preferred over outcome 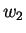 . Let
. Let ![$p,q \in [0,1]$](img31.png) and
and 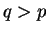 . Consider two outcomes
. Consider two outcomes
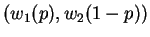 and
and
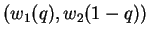 in
in 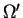 . A rational player should choose second outcome over the first. Formally :
. A rational player should choose second outcome over the first. Formally :
![$\forall w_1,w_2 \in \Omega,\,\forall p,q \in [0,1]$](img36.png) s.t.
s.t. 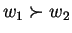 and
and 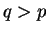 ,
,
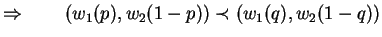
If outcome 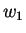 is preferred over outcome
is preferred over outcome 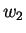 and outcome
and outcome 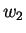 is preferred over outcome
is preferred over outcome 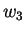 , then there exists a probability p, such that the player is indifferent to the outcome
, then there exists a probability p, such that the player is indifferent to the outcome
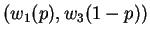 and
and 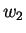 . Formally :
. Formally :
If
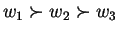 , then
, then
![$\exists p \in [0,1] \;$](img42.png) s.t.
s.t.
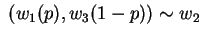
Corollary : For 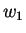 ,
, 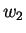 ,
, 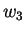 defined as above, there exists a unique
defined as above, there exists a unique
![$p \in [0,1] \;$](img44.png) s.t.
s.t.
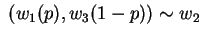 .
.
Proof : Suppose there exist
![$p_1,p_2 \in [0,1]$](img45.png) and
and 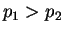 (without loss of generality) s.t.
(without loss of generality) s.t.
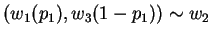 and
and
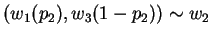
From first postulate, we know that:
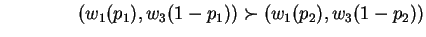
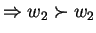 which is a contradiction.
which is a contradiction.
According to this postulate, if the player is indifferent between two outcomes say 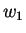 and
and 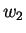 , and in another outcome say
, and in another outcome say 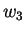 ,
, 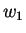 happens with probability
happens with probability 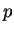 , then the player remains indifferent if
, then the player remains indifferent if 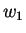 in
in 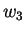 is replaced by
is replaced by 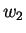 . To state this formally, label outcomes
. To state this formally, label outcomes
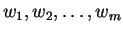 in
in 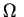 s.t.
s.t.
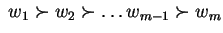 . Consider an outcome
. Consider an outcome 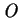 in
in 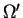 given as :
given as :
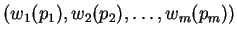
Let 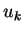 be the probability
be the probability  s.t.
s.t. 
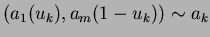 .
.
If
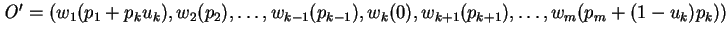 , then
, then
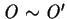
Von Neumann and Morgenstern utility function 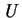 is defined over
is defined over
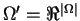 . Let
. Let
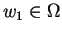 is the most preferred outcome
is the most preferred outcome
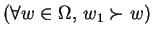 and
and
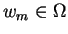 is the least preferred outcome
is the least preferred outcome
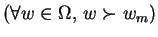 . For each outcome
. For each outcome 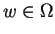 , define
, define
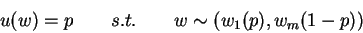 |
(1) |
From postulate 2, such a 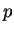 always exists and is unique.
always exists and is unique.
Von Neumann and Morgenstern utility function for
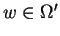 is the expected value of the utility function u() as defined by equation 2. i.e.
is the expected value of the utility function u() as defined by equation 2. i.e.
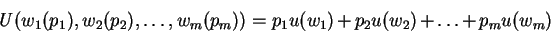 |
(2) |
To check that the Von Neumann and Morgenstern utility function represents the preference relationship on 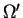 , consider two outcomes
, consider two outcomes 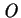 and
and
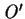 in
in
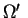 .i.e.
.i.e.
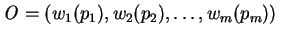 and
and
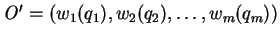
By repeated application of postulate 3, we get :
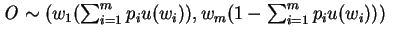 and
and
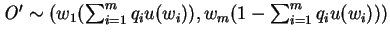
From postulate 1, it is clear that given two outcomes 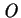 and
and
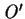 in
in 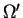 (as defined above), a rational player will prefer the one, which corresponds to higher expected value of the utility function, u().
(as defined above), a rational player will prefer the one, which corresponds to higher expected value of the utility function, u().
Therefore,
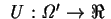 represents a preference relationship on
represents a preference relationship on 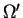 .
.



Vishrut Goyal
2002-10-01
![]() and
and ![]() ) from the set
) from the set ![]() , with outcome
, with outcome ![]() being preferred over outcome
being preferred over outcome ![]() . Let
. Let ![]() and
and ![]() . Consider two outcomes
. Consider two outcomes
![]() and
and
![]() in
in ![]() . A rational player should choose second outcome over the first. Formally :
. A rational player should choose second outcome over the first. Formally :
![]() s.t.
s.t. ![]() and
and ![]() ,
,
![]()
![]() is preferred over outcome
is preferred over outcome ![]() and outcome
and outcome ![]() is preferred over outcome
is preferred over outcome ![]() , then there exists a probability p, such that the player is indifferent to the outcome
, then there exists a probability p, such that the player is indifferent to the outcome
![]() and
and ![]() . Formally :
. Formally :
![]() , then
, then
![]() s.t.
s.t.
![]()
![]() ,
, ![]() ,
, ![]() defined as above, there exists a unique
defined as above, there exists a unique
![]() s.t.
s.t.
![]() .
.
![]() and
and ![]() (without loss of generality) s.t.
(without loss of generality) s.t.
![]() and
and
![]()
![]()
![]() which is a contradiction.
which is a contradiction.
![]() and
and ![]() , and in another outcome say
, and in another outcome say ![]() ,
, ![]() happens with probability
happens with probability ![]() , then the player remains indifferent if
, then the player remains indifferent if ![]() in
in ![]() is replaced by
is replaced by ![]() . To state this formally, label outcomes
. To state this formally, label outcomes
![]() in
in ![]() s.t.
s.t.
![]() . Consider an outcome
. Consider an outcome ![]() in
in ![]() given as :
given as :
![]()
![]() be the probability
be the probability ![]() s.t.
s.t. ![]()
![]() .
.
![]() , then
, then
![]()
![]() is defined over
is defined over
![]() . Let
. Let
![]() is the most preferred outcome
is the most preferred outcome
![]() and
and
![]() is the least preferred outcome
is the least preferred outcome
![]() . For each outcome
. For each outcome ![]() , define
, define