Games are classified as follows :-
Here the players are allowed to form coalitions to share decisions,
In such games the players follow the rationality assumption and play
There are 2 forms of non-cooperative games.
a) Extensive Form : Here the players make their moves in turns. There are
b) Normal Form : Here the game is one shot and the players make simultaneous moves.
The rows in the payoff matrix represent the strategies of player 1: S1, S2....Sn. The columns represent the strategies of player 2 : S1, S2, S3...Sm. Each element of the matrix represents payoffs for a particular outcome (combination of players' strategies) of the game. The Fig. below shown a general payoff matrix with payoffs of both players, denoted as (aij, bij). Here, aij represents the payoff for player 1 and bij represents the payoff for player 2 under strategy combination (Si, Sj).
A strategy profile, (w1*, w2*, ... wn*) constitutes a Nash Equilibrium, iff
For all i , wi : Ui(w1*, w2*,. ,wi*...wn*) >= Ui(w1*,w2*,...wi',...wn*)
In
a game where pure strategy is used Nash Equilibrium may or may not exist.
In the game of prisoner's dilemma (described in Lecture1), there is only one Nash Equilibirum, (Confess,Confess), i.e. both players will confess.
This can be proved as follows. When, P1 confesses, P2 is better off confessing than denying because he gets 5 years confessing which is less than 10 years
if he denies. When, P2 confesses, P1 is better off confessing than denying, because P1 gets 5 years when he confesses but he gets 10 years on denying. The above analysis, shows that (C,C) represents Nash Equilibrium. Similarly, one can show that this is the only Nash Equilibrium in this game.
Prisoner's Dilemma (Payoff Matrix)
Consider a husband and wife who have different plans to spend the evening together
and
have fun. The husband is interested in watching a cricket match while the
wife is interested in going out to watch a movie. We can model this as
a game with husband as first player (P1) and wife as the second player
(P2).
The payoff matrix for this game is given below. The pay-offs for both players in the four outcomes are explained here :-
a) When P1 and P2 both go for cricket, P1 has payoff of 10 because that
option was his preference, while P2 has payoff of 5 because cricket was
b) When P1 goes for cricket while P2 goes for movie, since they are separated from each other, the whole objective of having fun together gets defeated, so each ends up with a payoff of 1.
c) When P1 goes for movie and P2 goes for cricket, they go for something they don't prefer and also go alone, so each gets a negative payoff of -10.
d) When P1 goes for movie and P2 goes for movie, then since movie is P2's preference she gets payoff of 10, while P1 gets payoff of 5 because his preference was cricket.
On analysing this matrix, one can see that there are 2 Nash Equillibrium : (10,5) and (5,10).
Movie/Cricket Game (Outcome Matrix)
Consider, the following game of matching pennies. Here, 2 players, P1 & P2,
toss one coin each. If the result of toss is same for both players, then P1 wins
and gets payoff of 1, while P2 loses and gets payoff of -1. If the result of the toss
does not match between 2 players, then P2 wins with payoff of 1, while P1 loses and
gets payoff of -1. This is a zero sum game.
Matching Pennies (Payoff Matrix)
Constant
Sum Game (Payoff Matrix)
The cold war between US and USSR can also be modelled as a game. Both US and USSR have the option of spending their budget on health or defense and each of them would like to get strategic defense advantage over the other.
When,
both players spend on health they get payoff of 10 each. When, one spends
on health while the other spends on defense, the one who spends on health
gets payoff of -10, because the other one who spends on defence gets strategic
defence advantage and hence gets a payoff of 15. When both players spend
on defense, they each have payoff of 1 because then the country's health
suffers.
Here, it can easily be shown that there is only one Nash Equilibrium (D,D).
This game theoretic model seems to explain what happened during the cold war between US and USSR.
Consider a village with N farmers, that has limited grassland. Each of the N farmers have the option to keep a sheep. Let the utility of milk and wool from the sheep be 1. Let the damage to the environment from one sheep grazing over the grassland be denoted by -5.
Let Xi be a variable that takes values 0 or 1 and it denotes that whether the ith farmer keeps sheep or not.
Xi = 1, ith farmer keeps sheep
= 0, ith farmer does not keep sheep
So, the utility of the ith farmer, Ui(Xi), is given by :-
Ui(Xi ) = Xi - { [ 5 * (X1 + X2 + X3 + ..... Xn) ] / N }
since, the total environmental damage is shared by all farmers.
In this game, Xi = 1, is a Nash Equilibrium for all i, if N >= 5
and this Nash Equilibrium is unique if N > 5. This can be easily shown because keeping a sheep would add more utility to a farmer from milk/wool than subtract utility from him due to environmental damage. Thus, everyone will end up keeping a sheep and the utility for every farmer will be -4.
In real life this leads to excessive environmental damage. In this case, game theory comes to rescue to by justifying a pollution tax of keeping the sheep, of an amount equal to the damage done to the environment. So, when this pollution tax is added , the utility of the ith farmer becomes
Ui(X1,X2,...Xn) = Xi - 5Xi - { [5 * (X1 + X2 + X3 + ..... Xn) ] / N }
Now, in this case, the Nash Equilibrium is Xi = 0, for all i. This is because any farmer will increase his utility by giving away his sheep. Thus everyone will give away his sheep and each will have utility of 0.
The above example of tragedy of the commons can be used to explain large number of real life situations. Consider, the scenario of industries polluting the environment. Here, the industries can be considered as sheep and the environment can be considered as grassland and similar analysis of tragedy of commons holds true. In another scenario of illegal construction of houses causing infrastructure problems, the houses denote the sheep and the infrastructure denotes the grassland in the tragedy of the commons.
Thus, game theory can be used to design laws and mechanisms to get socially desirable outcomes.
The Traffic light model from game theoretic point of view was described in Lecture1. Here we re-visit the same model for the purpose of describing the behaviour of the system under the assumptions of increasing and decreasing marginal cost of delay.
The payoff matrix is shown below for reference.
Traffic Light (Outcome Matrix)
Here assuming that D >> d, C(d+D) = C(D) + d.C'(D),
where C'(D) is the first derivative of cost of delay C(D) w.r.t. D. That is it
represents the rate of change of cost of delay w.r.t. to delay.
The two cases of marginal cost of delay function are considered below :-
a) When the marginal cost of delay is a decreasing function, then the above game
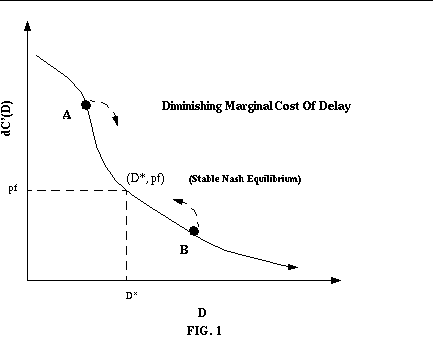
leads to convergence, as shown in Fig.1 below.
In the Fig.1 below, the y axis plots : d.C'(D), x-axis plots : D.
The point (D*, pf) is marked as an equillibrium point obtained as follows :-
Consider, point A in the Fig.1. A player at this point has dC'(D) more
than p(f) , so this player will tend to disobey => the value of D tends to move
Now consider point B. At this point, pf > dC'(D), so a player at this point will
tend to obey the traffic light and therefore wait => the congestion delay will tend
to reduce and move towards D*.
Therefore, the congestion in the system tends to move towards D*, the equillibrium point.
b) Now, consider the case when the marginal cost of delay is an increasing function. then the system tends towards chaos. In the Fig.2 given below, again focus on two points A & B.
At point A, dC'(D) > pf, so the player at this point tends to disobey and hence, moves in the direction away from D* => more traffic congestion.
At point B, dC'(D) < pf, so the player at this point tends to obey and hence the congestion drops further.
Thus, the players at points before and after D*, tend to move away from D*
and so the equillibrium is not reached.
Draw the game matrix for the repeated Prisoner's Dilemma and find the best strategy in the game. Consider 3 repetitions in the game, i.e. {C,D}3