


Next: About this document ...
Lecture 17
Multi Item auction
October 09, 2002 transcribed by Dhan Mahesh
In this class we would be discussing Multi Item Auction.
There are 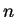 buyers and
buyers and 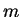 sellers each buyer wants to buy only one item
out of the many available. Each seller has a single item to sell.
sellers each buyer wants to buy only one item
out of the many available. Each seller has a single item to sell.
One of the scenarios is a market of second-hand cars where each seller
brings a car for sale. Buyers are interested in at most one car
each. Buyers have preferences over cars. Also depending on the price
of the car. So each buyer will rank car and assigns some value
to it.
For example:
| Car Model |
Value (in Lakhs) |
Price (in Lakhs) |
| Maruti 800 |
1.0 |
0.5 |
| Lancer |
5.0 |
1.0 |
Which car would a buyer prefer? How would his/her preference be represented?
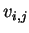 stands for the maximum a buyer
stands for the maximum a buyer 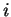 is willing to pay for item
is willing to pay for item  .
.
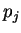 stands for the price at which item j can be bought.
stands for the price at which item j can be bought.
Buyers may want to maximize their surplus : 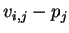 or the
profit ratio
or the
profit ratio 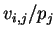
Every seller has a reserve price 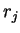 on item
on item  . The reserve
price represents the minimum price that a seller expects for the
item and he/she would like to maximize his/her surplus that is given
by
. The reserve
price represents the minimum price that a seller expects for the
item and he/she would like to maximize his/her surplus that is given
by 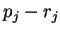
If the utilities are quasi linear in money then the social optimal
for the economy is to maximize the total surplus.
Define variable 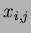 which is
which is 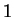 when buyer
when buyer 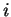 gets
item
gets
item  and
and 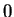 otherwise since each buyer can buy only one item.
otherwise since each buyer can buy only one item.
Also an item can be bought by atmost one buyer. Therefore
Surplus for buyer 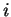 can be given by
can be given by
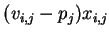 .The total buyer surplus is given by
.The total buyer surplus is given by

Similarly , total seller surplus is given by
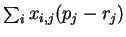
Therefore the total surplus given by
Note that the total surplus is independent of the prices. Therefore the problem of effecient allocation is same as finding maximum
weight matching in a bi partite graph matching with edge weights
equal to 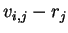 . This is formally stated as follows:
. This is formally stated as follows:
Maximum weighted bipartite matching gives allocation but the problem
of how much buyer has to pay to buy that item remains unsolved. Even
to get allocation also, one has to get teh maximum price a buyer is
willing to pay for an item and its reserve price from seller. Would
they give their current prices?
VCG procedure will give solution but let us see an alternative solution.
In the special case when 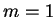 ( there is a single item) ascending english auction leads to efficient allocation.
( there is a single item) ascending english auction leads to efficient allocation.
Final price = Second highest value.
If two items and many buyers:
For example, two items and three buyers as below:
Let us assume reserve prices are zero.
Assume open cry ascending auction.
buyer 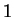 and buyer
and buyer 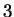 competes with eachother for item
competes with eachother for item 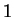 till Rs
till Rs 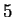 and then buyer
and then buyer 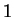 can outbid buyer
can outbid buyer 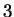 by quoting some price
by quoting some price 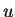 such
that
such
that 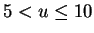 . Similarly in case of item
. Similarly in case of item 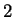 , buyer
, buyer 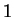 and
buyer
and
buyer 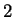 would be competing for item
would be competing for item 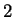 till Rs
till Rs 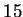 and then if
buyer
and then if
buyer 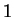 gets chance he/she has to decide which item to choose. It is
obvious that he/she would choose item
gets chance he/she has to decide which item to choose. It is
obvious that he/she would choose item 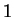 and gets it at some
and gets it at some 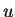 (
(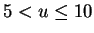 ). So buyer
). So buyer 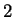 would get item
would get item 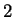 at some price
at some price 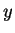 such that
such that
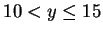 .
.
In general what procedure will give us stable and efficient
allocation? That procedure should lead to stable matching ( Self enforcing)
Bidding Procedure/strategy
General Case: At every step buyer 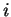 places a bid on item
places a bid on item  such that
such that 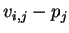 is maximized and then rests until somebody
outbids him/her.This procedure goes on like this. What will happen if
we go like this (sooner or later, bidding stops as price will come to
is maximized and then rests until somebody
outbids him/her.This procedure goes on like this. What will happen if
we go like this (sooner or later, bidding stops as price will come to 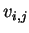 So, we are going to get with a matching and price. This procedure converges to (M,P)- (Matching, Price).
So, we are going to get with a matching and price. This procedure converges to (M,P)- (Matching, Price).
Theorem 0.1
Ascending Price simultaneous auctions lead to nearly
efficient allocations.[ Bertsekas ]
Stability:
A situation where when an auction terminates no buyer is interested in switching.
If this condition is not satisfied then 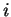 &
&  can deviate from
current allocation & be both better of , destabilizing X.
can deviate from
current allocation & be both better of , destabilizing X.
Claim: (M,P) is stable matching.
seller y tries to break up only if he gets more surplus. Buyer A tries
to break up only if he gets more surplus.
(A,y) would destabilize the matching iff
Let us see under what conditions we would get stable matching?
After A places bid on 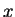 , price of
, price of 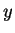 can increase (or stay
unchanged ). So his/her surplus on
can increase (or stay
unchanged ). So his/her surplus on 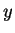 can't be more than on
can't be more than on 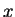 at a
future time. He/she placed a bid on
at a
future time. He/she placed a bid on 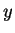 of
of 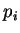 which is less that
which is less that 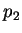
Lets see whether this leads to maximum surplus / efficient allocation ?
Assume number of buyers = number of items.
We would be getting a unique stable matching but lots of prices
possible.
Lets look at efficient allocation
![\includegraphics[width=0.35\textwidth]{fig52.eps}](img45.png) |
![\includegraphics[width=0.2\textwidth]{fig51.eps}](img46.png) |
| Fig 5(i): Our algo |
Fig 5(ii): Optimal (given by some other algo) |
So, each buyer will have 2 edges and each seller has 2 edges.
So, we would get some disjoint cycles. As there are equal number of
buyers and sellers, if we start from any buyer we will come back to
that buyer.
Now we have to prove that the sum of the weights picked by our algo is
atleast equal to that of Optimal.
add them up.
This is true for all the cycles. Therefore our algo will give the
correct maximum weighted bipartite matching.
If not all items are matched.
(assume for 3 buyers and 3 items)
add them up
but 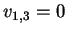 ;
;
another case:
Therefore our allocation gives better results.
So we can say that this procedure gives better results which are
competitive with respect to buyers and are stable
By VCG:
Take for every item each buyer is willing to pay and all the sellers
will sit and give to one who bids the maximum. We exclude that
bidder and find the price.
There can be different prices but same stable matching.
This method would be applicable for recruitment (employers and
employees).



Next: About this document ...
Dhan M Nakka
2002-11-26
![]() buyers and
buyers and ![]() sellers each buyer wants to buy only one item
out of the many available. Each seller has a single item to sell.
sellers each buyer wants to buy only one item
out of the many available. Each seller has a single item to sell.
![\includegraphics[width=0.4\textwidth]{figure1.eps}](img3.png)
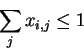
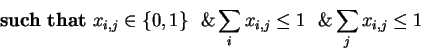
![]() ( there is a single item) ascending english auction leads to efficient allocation.
( there is a single item) ascending english auction leads to efficient allocation.
![\includegraphics[width=0.4\textwidth]{fig2.eps}](img27.png)
![]() &
& ![]() can deviate from
current allocation & be both better of , destabilizing X.
can deviate from
current allocation & be both better of , destabilizing X.
![\includegraphics[width=0.4\textwidth]{fig3.eps}](img36.png)
![\includegraphics[width=0.35\textwidth]{fig52.eps}](img45.png)
![\includegraphics[width=0.2\textwidth]{fig51.eps}](img46.png)
![\includegraphics[width=0.4\textwidth]{fig6.eps}](img47.png)
![\includegraphics[width=0.3\textwidth]{fig7.eps}](img52.png)
![\includegraphics[width=0.4\textwidth]{fig8.eps}](img58.png)