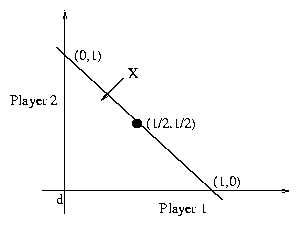Nash Bargaining Solutions
Scribe: Mayank Kumar & Tushar Chaudhary
Lecture 15: 25th September, 2002
1 Bargaining Solution
In a transaction
when the seller and the buyer value a product differently, a surplus is created.
A bargaining solution is then a way in which buyers and sellers agree to divide
the surplus.
For example, consider a house made by a builder A. It costed
him Rs.10 Lacs. A potential buyer is interested in the house and values it at
Rs.20 Lacs. This transaction can generate a surplus of Rs.10 Lacs. The builder
and the buyer now need to trade at a price. The buyer knows that the cost is
less than 20 Lacs and the seller knows that the value is greater than 10 Lacs.
The two of them need to agree at a price. Both try to maximize their surplus.
Buyer would want to buy it for 10 Lacs, while the seller would like to sell it
for 20 Lacs. They bargain on the price, and either trade or dismiss. Trade would
result in the generation of surplus, whereas no surplus is created in case of
no-trade. Bargaining Solution provides an acceptable way to divide the surplus
among the two parties.
Formally, a Bargaining Solution is defined as,
where X Í R2 and S,d Î
R2 . X represents the utilities of the players in the set of possible
bargaining agreements. d represents the point of disagreement.
In the above
example, price Î [10,20], bargaining set is simply x +
y £ 10, x ³ 0, y ³ 0. A point (x,y) in the bargaining set represents the case,
when seller gets a surplus of x, and buyer gets a surplus of y, i.e. seller
sells the house at 10 + x and the buyer pays 20 - y.
Assumption Bargainging Set X is convex and bounded.
 Figure 1: Bargaining Set
Figure 1: Bargaining Set
2 Pareto Optimality
A Pareto Optimal
solution is one in which none of the players can increase their payoff without
decreasing the payoff of atleast one of the other players.
A solution w is Pareto optimal iff
"w¢ Î W,
$i , s.t. ui(w¢) < ui(w), or "i ui(w¢) = ui(w) where
ui(w) is the utility function for player i
at outcome w.
All points on the boundary of the
Bargaining Set are Pareto Optimal solutions. In a bargaining situation, players
would like to settle at a pareto optimal outcome, because if they settle at an
outcome which is not pareto optimal, then there exists another outcome where
atleast one player is better off without hurting the interest of the other
players. Pareto optimal solutions are not unique in most of the cases.
Example. In the earlier example, x + y = 10 is a pareto optimal
frontier.
3 Properties of a Bargaining
Solution
Nash gave four axioms that any bargaining solution should satisfy.
- Invariant to affine transformations.
- Pareto optimality.
- Independence from Irrelevant Alternatives.
- Symmetry
- Invariant to affine transformations
An affine transformation
tAb : R2 ® R2 is defined by a matrix A, and a vector b of
the following form:
Now the transformation can be defined as:
A bargaining
solution is invariant to an affine transformation iff
"A, b, if
then
| F(tAb(X),tAb(d)) = tAb(S)
| |
- Pareto Optimality
F(X,d) should be a Pareto optimal solution.
Any bargaining solution should be better off than the disagreement
point.
- Independent from Irrelevant Alternatives
If S is the Nash
bargaining solution for a bargaining set X then for any subset Y of X
containing S, S continues to be the Nash Bargaining Solution. This axiom of
Nash is slightly controversial unlike the previous two axioms, since more
alternatives give you better bargaining power.
However, this can be
intuitively justified, by the folling argument:
Let us say that the set Y
has a NBS S' and S be another NBS of X (refer figure 2). Now S¢ Î Y, S Î Y and S¢ Î X, S Î X . In both the
bargaining sets X and Y, both the options S, S' are available to the players.
They should be expected to settle to the same outcomes. The presence of
irrelevant alternatives in X should not influence the bargaining solution.
Formally,
if
and
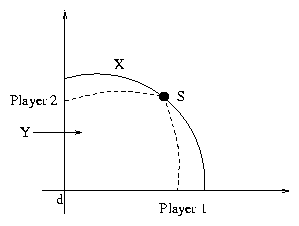 Figure 2: Independence from Irrelevant Alternatives
Figure 2: Independence from Irrelevant Alternatives
- Symmetry
The principle of symmetry says that symmetric utility
functions should ensure symmetric payoffs. Payoff should not discriminate
between the identities of the players. It should only depend on their payoff
functions. Put simply, symmetry implies the bargaining solution for region X =
x + y £ 1, x ³ 0, y ³ 0, d = (0,0) , should be (1/2,1/2) as shown in figure 3.
If both players have the same utility functions, then symmetry demands that
both get equal payoffs.
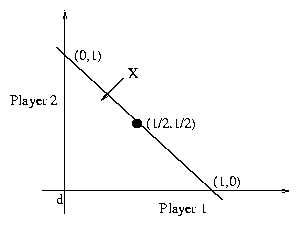 Figure 3: Symmetry
Figure 3: Symmetry
Nash characterized the NBS and proved that there is a unique
solution satisfying the axioms given by Nash.
Theorem: If a tangent is drawn to the curve defining
the boundary of the bargaining set at s - the Nash bargaining solution, it
intersects the lines parallel to the axes and passing through the disagreement
point (d) at points r and t. Then s = (r+t)/2 .
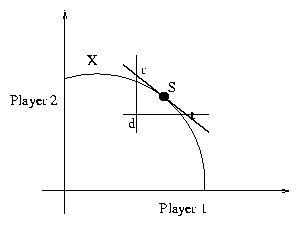 Figure 4: The bargaining solution s = (r+t)/2
Figure 4: The bargaining solution s = (r+t)/2
Proof: Let d = (d1,d2) where d1
and d2 are the utilities of the two players in the event of
disagreement. The bargaining problem is shown in Figure 4. Let S be a pareto
optimal point of X such that it is the midpoint of the line joining the points r
and t. We will prove that S is a NBS of (X,d).
Lets define an Affine
Function tAb where
and
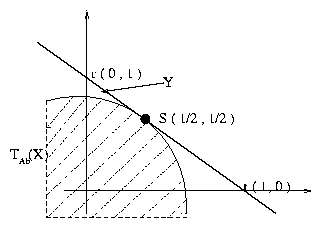 Figure 5:
Figure 5:
It is easy to see that
Let Y =
{(x1,x2):x1 + x2 £ 1, x1 ³ 0,
x2 ³ 0}. Note that tAb(s) is a NBS for (Y,0). Also, tAb(X) Ì Y (Since X is
convex), (0,0) Î tAb(X) , tAb(s) Î tAb(X) .
By Independence from irrelevant
alternatives, tAb(s) is a NBS for (tAb(X),tAb(d))
Therefore, s is a NBS for (X,d) , and
Generalised Nash
Bargaining Solution
If the players were asymetric in their bargaining
strengths, then NBS can be generalized by dropping the symmetry axiom. In this
case the NBS satisfies s=ar+bt
where a and b are bargaining
powers of the two players, and a+ b = 1
4 NBS as a Solution to the Alternating
Offers Game
Define the alternating offers game as an extensive form game (as
done in last lecture). In this game, two players bargain to settle on a price.
First of all player 1 makes an offer to player 2. Player 2 can either accept or
reject. If player 2 accepts the deal takes place, otherwise he incurs a discount
on his utility and makes an offer to the player 1. The game continues like this
until someone accepts the offer. Let u1(x) and u2(x), x
Î (0,1) be the utility functions of the two players. If
agreement settles in time t at x*, their payoff will be ( (d1)t u1(x*),
(d2)t
u2(x*) . The Subgame Perfect Equilibrium for this game is
defined by x* , y* s.t.
d1u1(x*) =
u1(y*)
d2u2(y*) =
u2(x*) Player 1 offers x* and accepts
any offer that is atleast y*. Similarly player 2 offers y*
and accepts anything that is atleast x*. If d1 = d2 =
d , then this is a symmetric game.
Theorem:
Nash Bargaining Solution is same as the solution to the symmetric
alternating offers game in the limit d® 1
Define Nash product as,
| g(x) = (x1 - d1)(x2 - d2)
| |
To prove the theorem we use
the following lemma.
Lemma. NBS S of (X,d) is the unique solution S
Î X that maximizes the Nash product g(x).
The proof
of this lemma is simple and can also be found in the prescribed text book.
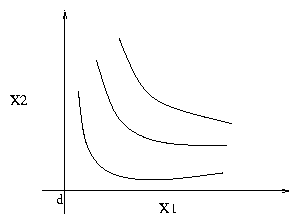 Figure 6: NBS maximizes g(x) = (x1-d1)*(x2-d2)
Figure 6: NBS maximizes g(x) = (x1-d1)*(x2-d2)
Let x*,y* correspond to the solutions of the
alternating offers game. Now,
Now,
In the
figure, the curve facing outward is the curve for g(x) = k, where k is a
constant. The farther we shift the curve from the origin, more value it attains.
Hence in the limiting case, the value of g(x) is maximum when it barely touches
the convex curve, i.e. x* = y*. In the limiting case, when
d is close to 1, x* = y*.
Therefore x* maximizes g(x) and x* Î X . Hence,
Þ x* is
Nash Bargaining Solution for (X,d).
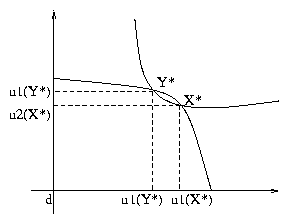 Figure 7: Correspondence with Repeated Game Bargain
Figure 7: Correspondence with Repeated Game Bargain
4.1 HomeWork
Say Rs.1 Lac was to be
divided between two players with the following utilities.
The bargaining set X is
given by (x1,x2): x1 + x2 £ 1, x1 ³ 0,
x2 ³ 0.
If x Î
[0,1], the utilities are given by
What is symmetric NBS
for this game and how does it depend on a, b? What can you conclude about the outcome of bargaining
between a risk neutral and a risk averse player?
File translated from TEX by TTH, version 3.21.
On 24 Nov 2002, 16:27.