Claim 1
There exists a value
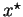
such that, in the SPE (Subgame
Perfect Equilibrium) of this game, player 1 proposes
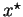
at
the first stage and player 2 accepts. That is in the scenario
discussed above, the best solution can be achieved in the first turn
itself.
Proof 1
The decision tree of the subgame perfect equilibrium can not be
infinite, because if it were to be so, both the players will get a
zero return in the end (as
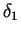
and
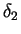
are both less
than 1 and
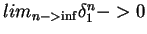
and
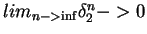
). If the first player were to offer anything more than zero
(in his first chance), player 2 being rational would have accepted
it, giving strictly better payoffs to both the players (thereby reducing the decision tree to just 1 level).
Now, let's assume that the subgame perfect equilibrium was attained after the
player 1's first offer was rejected by player 2. Let the game
terminate in n steps with an offer of
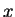
.The resultant payoffs for
the two player will be
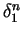
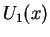
and
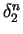
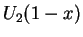
,
respectively. Now, since
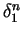
and
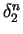
are both less than 1 and
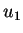
and
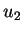
are both monotonically non-decreasing
functions, there exist a
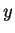
such that,
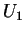 ( (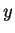 ) ) |
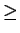 |
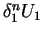 ( (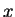 ) ) |
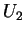 ( (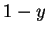 ) ) |
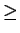 |
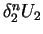 ( (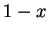 )
If player 1 will offer )
If player 1 will offer 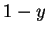 to player 2, the player 2 being
rational won't reject it, as she knows that if she rejects she will get to player 2, the player 2 being
rational won't reject it, as she knows that if she rejects she will get
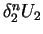 ( (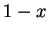 ), which is less than ), which is less than 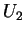 ( (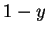 ). And since,
for player 1, ). And since,
for player 1, 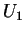 ( (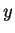 ) ) 
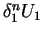 ( (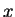 ), he will have
no hesitation in offering this to player 2. This will result in
termination of decision tree at the first level itself, which
contradicts the assumption taken above that subgame perfect
equilibrium was attained after the rejection of first proposal of
player 1 by player 2. Hence, it is proved that any subgame perfect
equilibrium can be achieved in the first turn itself. ), he will have
no hesitation in offering this to player 2. This will result in
termination of decision tree at the first level itself, which
contradicts the assumption taken above that subgame perfect
equilibrium was attained after the rejection of first proposal of
player 1 by player 2. Hence, it is proved that any subgame perfect
equilibrium can be achieved in the first turn itself. |
Proof 2
Let's assume that the final outcome in a subgame perfect equilibrium
where player 2 makes the first offer is
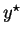
. So, in the game
where the first offer is to be given by player 1, if he were to give
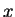
such that
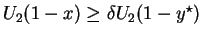
, player 2 being
rational will accept. However, if player 1 offers an x:
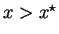
(where
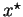
is a critical value for which ,
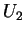
(
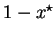
)
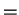
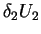
(
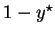
)), player 2 will
reject the offer, as she knows that since in the SPE where she makes
the first offer, the outcome is
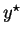
, she can always expect to
get a payoff of
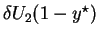
. On the other hand, if
player 1 were to offer an x:
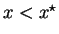
, he knows that he can get
a better payoff by offering
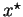
as
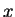
<
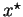
->
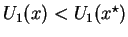
. This implies that player 1 being rational, will offer
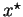
which will be accepted by player 2.
Now, consider the SPE where player 2 is to make his first offer. We
have already assumed it's outcome to be
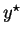
. However, for
player 1 to accept this offer,
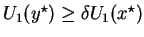
. Also, among all outcomes accepted by player 1, player
2 will offer the least possible, as
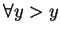
' (where
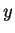
' is
such that

'
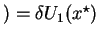
,
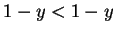
' and so,
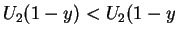
'
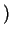
. So,
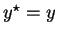
'. Therefore, the final
outcome of the SPE will either be
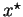
or
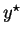
, depending
on whether player 1 proposes first or player 2 and
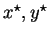
satisfies
![\includegraphics[width=5cm,height=4cm]{lin.eps}](img1.png)
![\includegraphics[width=5cm,height=4cm]{lin.eps}](img1.png)
![\includegraphics[width=5cm,height=4cm]{nonlin.eps}](img2.png)
![\includegraphics[width=5cm,height=4cm]{pareto.eps}](img17.png)
![\includegraphics[width=6cm,height=6cm]{subgame0.eps}](img29.png)
![\includegraphics[width=6cm,height=4cm]{subgame1.eps}](img38.png)