![\includegraphics[width=1.0\textwidth]{gt}](img1.png)
Scribed By: Mayank Bansal
In the previous lecture, we discussed the various means/methods of carrying out a Single Item Auction. We will now discuss how a Single Item Auction can be classified.
A Single-Item Auction can be classified into two types namely Sealed-Bid and Progressive depending upon the way the auction is conducted. In the Sealed-Bid Auction, the auctioneer invites sealed bids from the bidders, while in the Progressive Auction, the auction is carried out in the open where the bidders are asked to bid before everybody else. The Sealed Bid Auction can further be classified into two types: the First Price and the Second Price auctions. In the First Price auction, the item is given to the highest bidder at his own bid-value while in the Second Price auction, the item is given again to the higest bidder but at the bid value of the second highest bidder. The Progressive Auction can also be classified into two types namely the Ascending English Open-Cry Auction and the Descending Dutch Auction. In the Ascending English Open-Cry auction, the bidding starts at zero price and the bidders keep on out-bidding each other by increasing the bid value (the bid keeps on increasing) till only one bidder is left who gets the item. On the contrary, in the Descending Dutch auction, the bidding starts at a particularly high value set by the auctioneer. The auctioneer keeps on decreasing the price of the item till some bidder raises hand and agrees to buy the item at that price. The classification, has been depicted below:
![\includegraphics[width=1.0\textwidth]{gt}](img1.png)
There are two models under which a single-item auction can be considered viz. private known value model and common value model. In the private known value model the value that a bidder attaches to an item is independent of what values other bidders assign. In the common value model, the value attached by a bidder also depends upon what values other bidders assign. In all auction procedures, we will assume that bidders have private known values.
Let us now compare the various Bidding Mechanisms:
Now, consider a Second Price Auction. Here the highest bidder gets the item at the price equal to the second highest bidder's value. Also, ![]() (i.e. bidding true value) is a dominant strategy in the Second Price (and the English Open-Cry) Auction(s). The expected revenue, if
(i.e. bidding true value) is a dominant strategy in the Second Price (and the English Open-Cry) Auction(s). The expected revenue, if ![]() is
is
![]() . Note that both give the same expected revenue. Revenue equivalence holds for the general case as well.
. Note that both give the same expected revenue. Revenue equivalence holds for the general case as well.
The Descending Dutch Auction is similar to the First Price Auction. Here also the strategy is to choose a bid value ![]() and raise hand when the price,
and raise hand when the price, ![]() reaches
reaches ![]() .
.
Let ![]() represent the quantity of commodity
represent the quantity of commodity ![]() with the player
with the player ![]() .
.
![]() represents the utility function of player
represents the utility function of player ![]() and is assumed to be quasi-linear in commodity
and is assumed to be quasi-linear in commodity ![]() (money), i.e.
(money), i.e.
The procedure is the following:
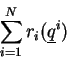
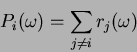
Lets look at the players' behaviour now. Player ![]() needs to:
needs to:
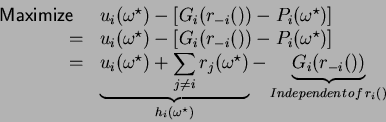
Since
![]() is independent of
is independent of ![]() and only depends on the value of
and only depends on the value of
![]() ,
, ![]() is maximized only if
is maximized only if
![]() maximizes
maximizes
![]() , which happens only if
, which happens only if ![]() .
.
So, we conclude that if the clearing house follows the above VCG procedure, then each player's payoff is maximized when his/her reported utility is equal to his/her true utility.
One choice of ![]() could be,
could be,
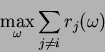
Now we see how Second Price, single item auctions can be modelled as a special case of VCG procedures.
Let us consider an auction with only one item and ![]() bidders. Let
bidders. Let ![]() mean that bidder
mean that bidder ![]() gets the item. Thus, an allocation
gets the item. Thus, an allocation ![]() would be,
would be,
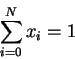
The utility function of player ![]() is a single number
is a single number ![]() . If the value attached to the item by the bidder is
. If the value attached to the item by the bidder is ![]() then the utility is given by,
then the utility is given by,
Let bidder ![]() bid a value
bid a value ![]() , then the reported utility is given by,
, then the reported utility is given by,
By VCG procedures, the clearing house (here the auctioneer) calculates a value
![]() s.t.
s.t.
![]() is maximized.
is maximized.
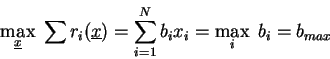
Let,
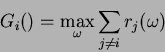
Thus, we can see that,
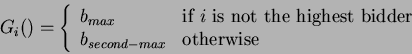
Now, it can be easily seen that,

So, the payment by the ![]() bidder to the auctioneer is given by,
bidder to the auctioneer is given by,
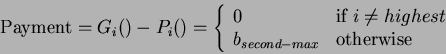
i.e. the payment is ![]() if
if ![]() and
and
![]() if
if ![]() .
.
Thus, we see that the VCG procedure correctly predicts that a single item auction will work as per Second Price auction procedure in that the highest bidder will get the item at the price of the second highest bidders value.