Learning Qualitative Models of U-tubes
Contents and links
Introduction to qualitative modelling and the U-tube
problem
Qualitative models are often better suited for several tasks than traditional
quantitative (numeric) methods. These tasks include diagnosis, generating
explanations of a system's behaviour and designing novel devices from first
principles. A more fundamental problem in the theory of dynamic systems
is the identification of the system itself. The basic problem is as follows.
We are given examples of the behaviour of a dynamic system. We want to
find a model that explains these examples. Accomplishing this, even at
the qualitative level, is quite difficult.
As an example, consider a ``U-tube'' system which consists just of two
containers connected by a tube as shown below:
Even a system as simple as this can have almost almost 195,000 possible
qualitative states when using a QSIM formalism, yet very few (only 32)
of these are actually ``legal''.
Learning legal states of a system
The problem addressed by the datasets provided here is to learn rules that
identify the legal states of this system. These rules, along with built-in
assumptions of continuity in QSIM, are sufficient to identify the dynamics
of the system.
Golem dataset
This requires determinate, ground background knowledge: experiments and
results are reported in [Bratko I., Muggleton S. and
Varsek A. (1992).
-
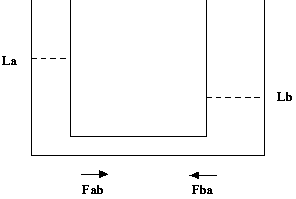
The target predicate is the relation state(La,Lb,Fab,Fba), where
La, Lb, Fab and Fba are as shown in
the figure.
-
The background knowledge is a tabulation of QSIM constraint primitives.
-
Consistency of infinite values in the add constraint can be ignored
for this problem. Further, since add requires a very large number
of ground facts, it is represented by three more efficient predicates.
norm_mag/4 normalises a qualitative value with respect to a landmark.
lookup_consist_table/3 is a lookup table for adding signs. verify_add_deriv/3
is a lookup table for adding directions of derivatives.
-
Additional background predicates provide range information. The QSIM constraints
m_plus/2 and m_minus/2 were only tabulated for empty
lists of corresponding values. All arguments of the background predicates
are of the same type; they are compound terms of the form
Func : QualValue/DirOfChange
The data used in these experiments is contained in one
compressed TAR file.
The Progol dataset
This data is more recent than the Golem data, and does not require the
background to be determinate or ground. Consequently, the background knowledge
fits QSIM practice more closely, consisting of QSIM predicate definitions
as described in [Kuipers B. (1986)]. All the data
used in these experiments is contained in one
compressed .pl file .
Recent work and its implications for biological modelling
The Progol experiments described above are unrealistic on the following
counts: (1) All levels were provided as part of the state description.
This allows the QSIM definitions to be treated deterministically by Progol.
Normal qualitative modelling practice would only provide the levels in
the two arms and the flow in one direction; (2) Positive and negative examples
were provided. The definition of negative examples is unnatural in this
domain, as only positive examples of behaviour are observable; and (3)
Examples presented required expert guidance (here, Ivan Bratko). Each of
these shortcomings has been rectified in recent work that constructs a
model using all positive examples of the behaviour of a u-tube. Examples
do not require all levels to be provided -- these are now introduced automatically
by Progol. The ability to construct autumatically models only using observed
levels and flows can have interesting applications in biological modelling.
For example, new experimental techniques are beginning to make available
large amounts of information about the transcriptome, proteome and metabolome
of organisms. This ``TPM'' data typically has many variables but few time-points,
and is unsuitable for traditional quantitative modelling. Qualitative models,
much like the simple u-tube, are still obtainable, and can form the first
step in extracting insight from the data. Initial trials of this are now
being undertaken using data from DeRise (1997)
Bibliography
Bratko I., Muggleton S. and Varsek A.
(1992).
Learning Qualitative Models of Dynamic Systems
in S. Muggleton editor. Inductive Logic Programming, Academic
Press, London.
DeRise J.L., Vishwanath R.I., and Brown
P.O.(1997).
Science, volume 278, pages 680-686
Kuipers B. (1986).
Qualitative simulation
in Artificial Intelligence, volume 29, pages 289--338.
Up to applications main page.

