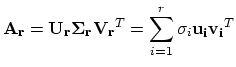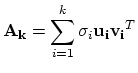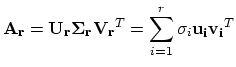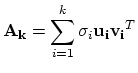

Next: Least-squares
Up: CSL361 Problem set 5:
Previous: CSL361 Problem set 5:
- Work out again the SVD theorem done in the class:
If 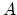 is a real
is a real
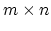 matrix then here exist orthogonal
matrices
matrix then here exist orthogonal
matrices
and
![$\displaystyle {\bf V} = \left[{\bf v_1},\ldots,{\bf v_n}\right] \in \mathbb{R}^{n \times n}
$](img4.png)
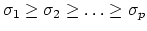 .
.
- Suppose that
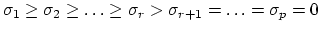 . Then show that
. Then show that
-
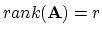
-
![$ null({\bf A}) = \left[{\bf v_{r+1}},\ldots,{\bf v_n}\right]$](img10.png)
-
![$ range({\bf A}) = \left[{\bf u_1},\ldots,{\bf u_r}\right]$](img11.png)
- If
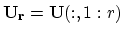 ,
,
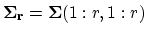 and
and
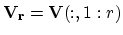 , then
, then
- Show that
-
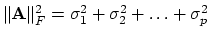
-
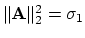
- Let the SVD of
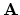 be as above. If
be as above. If
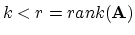 and
then show that
and
then show that
- Show (without using condition numbers) that if
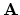 is square (
is square (
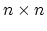 ) and
) and
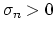 is
small, then solving
is
small, then solving 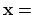 A
A
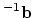 is unstable.
is unstable.
- Show that in the
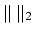 norm
norm
Subhashis Banerjee
2005-10-03
![$\displaystyle {\bf V} = \left[{\bf v_1},\ldots,{\bf v_n}\right] \in \mathbb{R}^{n \times n}
$](img4.png)
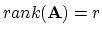
![$ null({\bf A}) = \left[{\bf v_{r+1}},\ldots,{\bf v_n}\right]$](img10.png)
![$ range({\bf A}) = \left[{\bf u_1},\ldots,{\bf u_r}\right]$](img11.png)
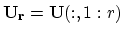 ,
,
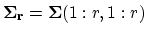 and
and
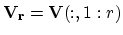 , then
, then